هر نقطه داده را به عنوان یک گره در یک نمودار و شباهت بین نقاط داده را به عنوان یال هایی که آن گره ها را به هم متصل می کنند، تصور کنید. خوشهبندی طیفی مقادیر ویژه و بردارهای ویژه یک ماتریس به دست آمده از این نمودار را برای شناسایی الگوها و گروهبندیهای معنیدار درون دادهها تجزیه و تحلیل میکند.
در اصل، خوشهبندی طیفی روشی قدرتمند برای یافتن گروهبندیهای طبیعی در دادهها است، بهویژه زمانی که خوشهها ممکن است اشکال پیچیده داشته باشند یا زمانی که الگوریتمهای خوشهبندی سنتی ممکن است مشکل داشته باشند.
این خوشه بندی در نهایت هر الگوریتم خوشه بندی (K – Means) استفاده میکند اما قبل از آن یکسری تغییرات در داده ها ایجاد می کند
این نوع الگوریتم خوشه بندی باعث می شود که خوشه ها به صورت شکل هایی درست شوند که نقاط نزدیک و متصل بهم در یک خوشه قرار بگیرند
خوشه بندی طیفی برای خوشه بندی داده ها با ابعاد بسیار بالا استفاده میشود با استفاده از اتصال نقاط داده
مجموعه های داده ای که ساختار مشخصی ندارند و ممکن است دیگر روش های خوشه بندی مانند (K- Means) و (K-Mediods) و … موثر نباشند از خوشه بندی طیفی استفاده میکنیم
در خوشه بندی طیفی نقاط داده را به فضایی با ابعاد پایین تر تبدیل میکنیم , این تبدیل با استفاده از تکنیک های طیفی مانند نمودار لاپلاسین یا تجزیه ویژه انجام میشود
وقتی داده هارا به ابعاد کوچکتر تبدیل کردیم می توانیم الگوریتم های دیگر خوشه بندی را روی آنها پیاده سازی کنیم
خوشهبندی یکی از پرکاربردترین تکنیکها برای تجزیه و تحلیل دادههای اکتشافی است که کاربردهایی از آمار، علوم کامپیوتر، زیستشناسی تا علوم اجتماعی یا روانشناسی دارد. افراد سعی می کنند با شناسایی گروه هایی از “رفتار مشابه” در داده های خود، اولین برداشت را از داده های خود به دست آورند.
خوشه بندی طیفی یک تکنیک EDA است که مجموعه داده های پیچیده چند بعدی را به خوشه هایی از داده های مشابه در ابعاد نادرتر کاهش می دهد. طرح اصلی این است که طیف وسیعی از نقاط داده سازمانیافته را به گروههای متعدد بر اساس منحصربهفرد بودن آنها خوشهبندی کنیم. (یعنی نقاط داده) که به هم متصل یا بلافاصله در کنار یکدیگر هستند در یک نمودار مشخص می شوند. سپس گره ها به فضایی با ابعاد کم نگاشت می شوند که به راحتی می توان آن ها را برای تشکیل خوشه ها جدا کرد. خوشهبندی طیفی از اطلاعات مقادیر ویژه (طیف) ماتریسهای خاص (مانند ماتریس قرابت، ماتریس درجه و ماتریس لاپلاسی) استفاده میکند که از نمودار یا مجموعه دادهها مشتق شدهاند.
📌 تفاوت بین خوشه بندی طیفی و تکنیک های خوشه بندی قبلی
خوشه بندی طیفی انعطاف پذیر است و به ما اجازه می دهد تا داده های غیر گرافیکی را نیز خوشه بندی کنیم. هیچ فرضی در مورد شکل خوشه ها نمی کند. تکنیک های خوشه بندی، مانند K-Means، فرض می کنند که نقاط اختصاص داده شده به یک خوشه در مرکز خوشه کروی هستند. این یک فرض قوی است و ممکن است همیشه مرتبط نباشد. در چنین مواردی، Spectral Clustering به ایجاد خوشه های دقیق تر کمک می کند. می تواند مشاهداتی را که در واقع به همان خوشه تعلق دارند، اما به دلیل کاهش ابعاد، دورتر از مشاهدات سایر خوشه ها هستند، به درستی خوشه بندی کند.
نقاط داده در خوشهبندی طیفی باید به هم متصل باشند، اما ممکن است لزوماً دارای مرزهای محدب نباشند، برخلاف تکنیکهای خوشهبندی مرسوم، که در آن خوشهبندی بر اساس فشردگی نقاط داده است. اگرچه، از نظر محاسباتی برای مجموعه داده های بزرگ گران است، زیرا مقادیر ویژه و بردارهای ویژه باید محاسبه شوند و خوشه بندی روی این بردارها انجام می شود. همچنین، برای مجموعه داده های بزرگ، پیچیدگی افزایش می یابد و دقت به طور قابل توجهی کاهش می یابد.
📌 مراحل پیاده سازی الگوریتم Spectral Clustring
ماتریس وابستگی یا شباهت :
اولین مرحله ایجاد ماتریسی است که نشان دهنده شباهت یا قرابت بین هر جفت نقطه داده است. این ماتریس اغلب به عنوان ماتریس میل نامیده می شود. انتخاب معیار تشابه به ماهیت داده های شما بستگی دارد.
این ماتریس یک ماتریکس nxn است که n تعداد نمونه ها است . سلول ها را با فاصله اقلیدوسی پر میکنیم
این ماتریس شباهت ها یا فواصل زوجی بین نقاط داده را نمایش میدهد . روش های رایج برای ساخت این ماتریس استفاده از (Gaussian Kernel),(K-nearest-neigbors) و رویکرد مبتنی بر گراف است
در قسمت زیر فرمول Gaussian Kernel را خواهیم دید که برای محاسبه ی فاصله ی دو نقطه از آن استفاده میکنیم
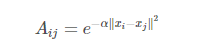
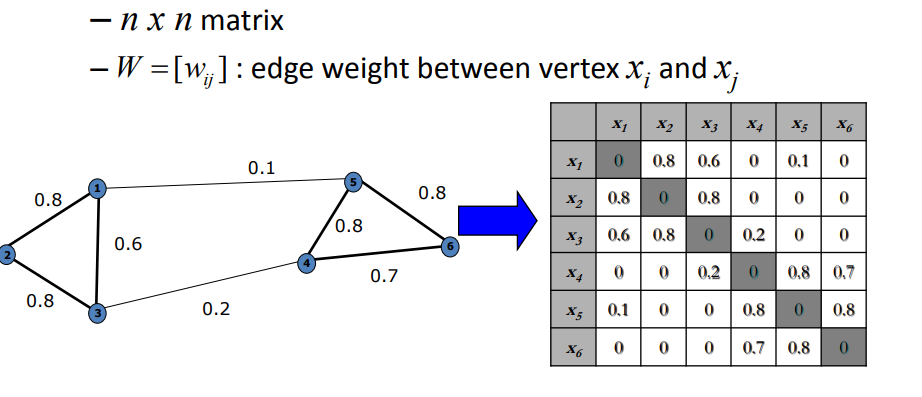
نحوه ی عملکرد آن :
با توجه به مجموعه ای از نقاط داده x1،…xn و تصوری از شباهت sij ≥ 0 بین همه جفت نقاط داده xi و xj، هدف شهودی خوشه بندی تقسیم نقاط داده به چند گروه است، به طوری که نقاط در یک گروه مشابه باشند. مشابه و نقاط در گروه های مختلف با یکدیگر بی شباهت هستند. اگر اطلاعاتی بیش از شباهت بین نقاط داده نداشته باشیم، یک راه خوب برای نمایش داده ها به شکل نمودار شباهت G = (V,E) است. هر رأس vi در این نمودار نشان دهنده یک نقطه داده xi است. اگر شباهت sij بین نقاط داده متناظر xi و xj مثبت یا بزرگتر از یک آستانه معین باشد، دو راس به هم متصل می شوند و یال با sij وزن می شود. مشکل خوشهبندی را میتوان با استفاده از نمودار شباهت دوباره فرمولبندی کرد: ما میخواهیم پارتیشنی از نمودار پیدا کنیم که یالهای بین گروههای مختلف وزن بسیار کمی داشته باشند (به این معنی که نقاط در خوشههای مختلف با یکدیگر متفاوت هستند) و یالها. در یک گروه وزن های بالایی دارند (به این معنی که نقاط درون یک خوشه مشابه یکدیگر هستند).
📌نمادها و تعاریف نمودار
نمودار ساده: یک گراف بدون جهت و بدون وزن که فاقد حلقه یا لبه های متعدد است.
گراف جهت دار: یک گراف G(V,E) با مجموعه ای از رئوس V و یک مجموعه E از جفت های مرتب شده از رئوس، به نام کمان، یال های جهت دار یا فلش. اگر (u,v) ∈ E می گوییم u به سمت v اشاره می کند. نقطه مقابل گراف جهت دار یک گراف بدون جهت است.
گراف جهت دار: گراف جهت دار بدون جفت یال های جهت دار متقارن.
نمودار کامل: یک نمودار ساده که در آن هر جفت رئوس متمایز توسط یک یال منحصر به فرد به هم متصل شده اند.
مسابقات: یک نمودار کامل جهت دار
مربع گراف: مربع گراف جهت دار G = (V,E) نمودار G2 = (V,E2) است به طوری که (u,w) ∈ E2 اگر و فقط اگر (u,v),(v, w) ∈ E.
ترتیب یک نمودار: ترتیب یک گراف G = (V,E) تعداد کل رئوس G است، یعنی |V|.
در درجه یک راس: تعداد یال هایی که در یک گراف جهت دار به یک راس می آیند. درجه نیز نوشته شده است.
نمودار منتظم: یک نمودار ساده که در آن درجه خارج از هر رأس برابر است. نمودار خارج از قاعده نیز نامیده می شود. در یک نمودار تقریباً (خارج از) منظم، هیچ دو درجه خارج بیش از یک با هم تفاوت ندارند.
خارج از درجه یک راس: تعداد یال هایی که از یک راس در یک نمودار جهت دار خارج می شوند. همچنین املای درجه بالاتر.
درخت: گرافی که در آن هر دو رأس دقیقاً توسط یک مسیر ساده به هم متصل می شوند. به عبارت دیگر، هر گراف متصل بدون چرخه یک درخت است.
برگ: یک راس u ∈ V به طوری که مجموع درجه خارج و درجه u دقیقاً 1 باشد.
جنگل: اتحاد ناقص درختان.
چرخه جهت دار: چرخه ای از لبه ها که همگی در یک جهت هدایت می شوند. چرخه جهت دار نیز نامیده می شود.
📌محاسبه ی گراف لاپلاسین :
از ماتریس شباهت مشتق گرفته شده است و روابط بین نقاط را نمایش میدهد
انواع مختلفی از ماتریس لاپلاس وجود دارد مانند و روشهای متداول شامل لاپلاسی غیرعادی، لاپلاسی نرمالشده یا لاپلاسی با راه رفتن تصادفی است.
در قسمت پایین فرمول أنواع لاپلاس را مشاهده خواهیم کرد :

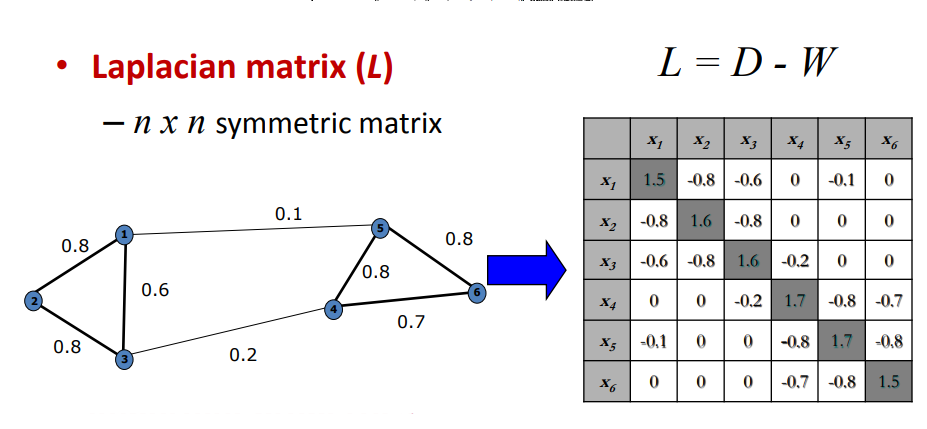
📌محاسبه ی بردار ویژه :
مربوط به کوچکترین مقادیر ویژه ماتریس لاپلاسی محاسبه میشود
این بردار های ویژه نمایشی با ابعاد پایین تر از داده ها را تشکیل میدهند
تعداد مقادیر ویژه و بردارهای ویژه ای که انتخاب می کنید به تعداد خوشه های مورد نظر بستگی دارد.
📌با بردارهای ویژه یک ماتریس تشکیل دهید
بردارهای ویژه انتخاب شده به عنوان ستون، ماتریسی تشکیل دهید. این ماتریس برای نمایش داده ها در فضایی با ابعاد کمتر استفاده خواهد شد.
مثال: اگر اولین k بردارهای ویژه را انتخاب کنید، جایی که k تعداد خوشه هایی است که می خواهید، یک ماتریس با این ستون های k ایجاد می کنید.
📌خوشه بندی در فضا با ابعاد پایین
الگوریتم های خوشه بندی سنتی مانند K-means برای اختصاص دادن نقاط داده به خوشه ها بر بردار های ویژه اعمال میشوند
📌بازگشت خوشه های نقشه به فضای اصلی:
هنگامی که خوشه ها در فضای با ابعاد پایین تر مشخص شدند، آنها را به فضای اصلی برگردانید تا نتیجه خوشه بندی نهایی را به دست آورید.
مثال: برای شناسایی خوشه ها در داده های اصلی، از نقشه برداری از فضای با ابعاد پایین به فضای اصلی استفاده کنید.
خوشه بندی طیفی برای گرفتن روابط پیچیده و ساختارهای غیر خطی در داده ها موثر است. انتخاب پارامترها، مانند تعداد خوشه ها و اندازه گیری وابستگی، نیاز به تنظیم بر اساس ویژگی های داده های شما دارد
📌پیدا کردن مقدار k :
تفاوت بین دو مقدار ویژه متوالی
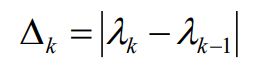
پایدارترین خوشه بندی عموماً با مقدار k داده می شود که بیان را به حداکثر می رساند
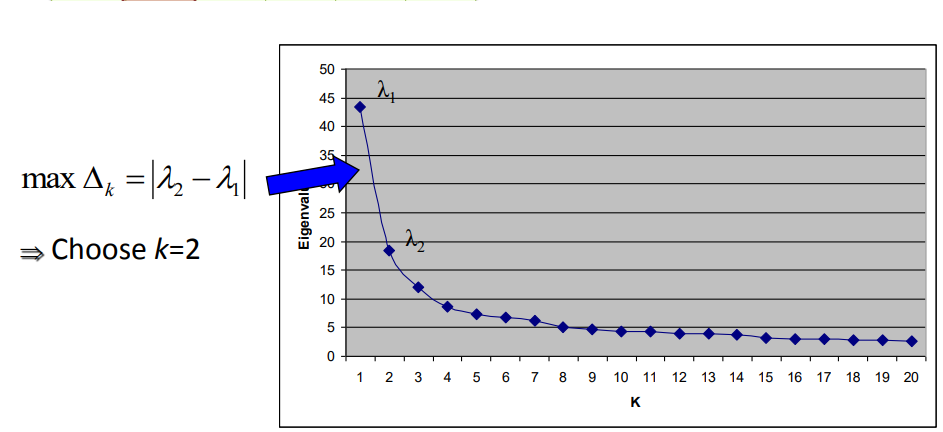
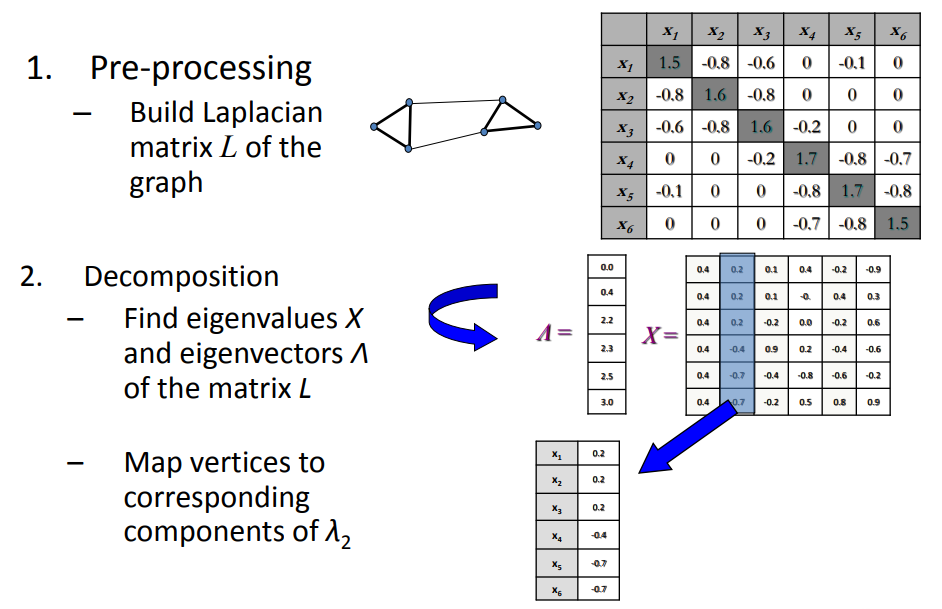
ماتریسی که بردار ویژه لاپلاسی را نشان می دهد (بردار ویژه مطابق با مقادیر ویژه متناظر با ترتیب افزایشی)
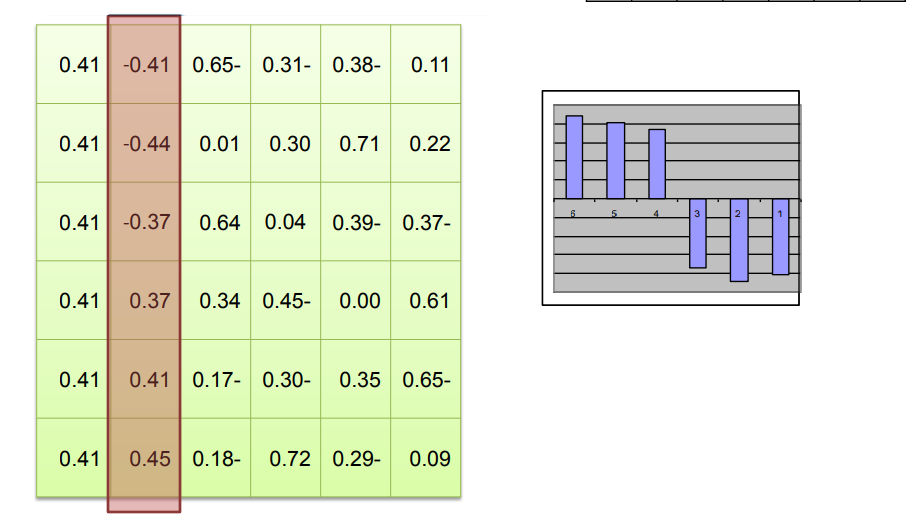
گروه بندی
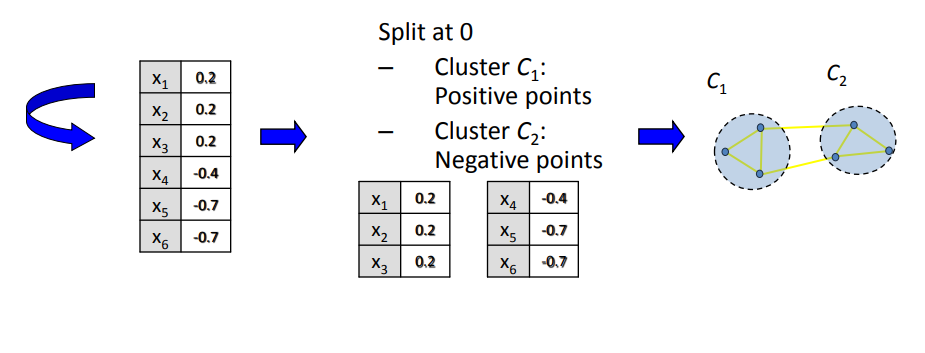
– مرتب سازی اجزای بردار 1 بعدی کاهش یافته
– خوشه ها را با تقسیم بردار مرتب شده به دو قسمت شناسایی کنید (بالای صفر، زیر صفر)
📌کجا می توانم از خوشه بندی طیفی استفاده کنم؟
خوشه بندی طیفی در بسیاری از زمینه ها کاربرد خود را شامل می شود:
تقسیم تصویر ، داده های آموزشی کاوی ، وضوح موجودیت ، جداسازی گفتار ، خوشه بندی طیفی توالی پروتئین ، تقسیم تصویر متن.
اگرچه خوشه بندی طیفی تکنیکی است که بر اساس تئوری نمودار ساخته شده است ، از این رویکرد برای شناسایی جوامع راس ها در یک نمودار بر اساس لبه های متصل به آنها استفاده می شود. این روش انعطاف پذیر است و به ما امکان می دهد تا داده های غیر Graph را نیز با داده های اصلی یا بدون آن جمع کنیم.
PythonExample
import numpy as np
l = 100
x, y = np.indices((l, l))
center1 = (28, 24)
center2 = (40, 50)
center3 = (67, 58)
center4 = (24, 70)
radius1, radius2, radius3, radius4 = 16, 14, 15, 14
circle1 = (x - center1[0]) ** 2 + (y - center1[1]) ** 2 < radius1**2
circle2 = (x - center2[0]) ** 2 + (y - center2[1]) ** 2 < radius2**2
circle3 = (x - center3[0]) ** 2 + (y - center3[1]) ** 2 < radius3**2
circle4 = (x - center4[0]) ** 2 + (y - center4[1]) ** 2 < radius4**2
img = circle1 + circle2 + circle3 + circle4
# We use a mask that limits to the foreground: the problem that we are
# interested in here is not separating the objects from the background,
# but separating them one from the other.
mask = img.astype(bool)
img = img.astype(float)
img += 1 + 0.2 * np.random.randn(*img.shape)
from sklearn.feature_extraction import image
graph = image.img_to_graph(img, mask=mask)
graph.data = np.exp(-graph.data / graph.data.std())
import matplotlib.pyplot as plt
from sklearn.cluster import spectral_clustering
labels = spectral_clustering(graph, n_clusters=4, eigen_solver="arpack")
label_im = np.full(mask.shape, -1.0)
label_im[mask] = labels
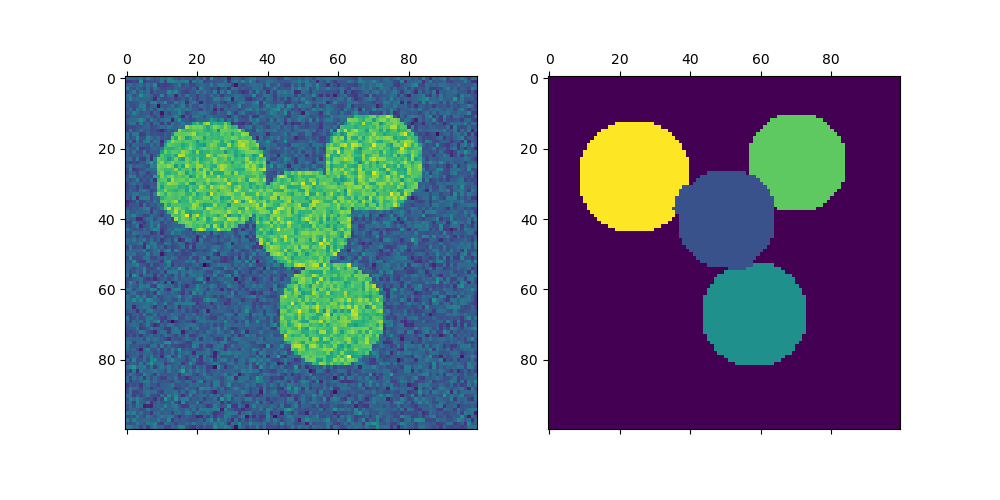
fig, axs = plt.subplots(nrows=1, ncols=2, figsize=(10, 5))
axs[0].matshow(img)
axs[1].matshow(label_im)
plt.show()
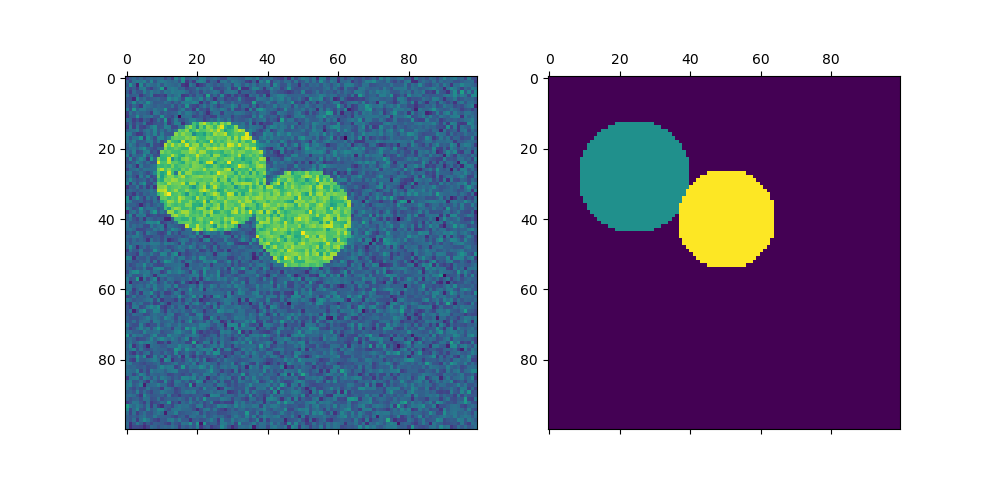
img = circle1 + circle2
mask = img.astype(bool)
img = img.astype(float)
img += 1 + 0.2 * np.random.randn(*img.shape)
graph = image.img_to_graph(img, mask=mask)
graph.data = np.exp(-graph.data / graph.data.std())
labels = spectral_clustering(graph, n_clusters=2, eigen_solver="arpack")
label_im = np.full(mask.shape, -1.0)
label_im[mask] = labels
fig, axs = plt.subplots(nrows=1, ncols=2, figsize=(10, 5))
axs[0].matshow(img)
axs[1].matshow(label_im)
plt.show()