یادگیری نیمه‌نظارت‌شده چیست؟

مقدمه

در بسیاری از مسائل واقعی یادگیری ماشین، دسترسی به حجم زیادی از داده‌های خام وجود دارد. اما برچسب‌گذاری دقیق این داده‌ها اغلب پرهزینه، زمان‌بر و نیازمند تخصص انسانی است. در چنین شرایطی، استفاده صرف از یادگیری نظارت‌شده یا نظارت‌نشده به‌تنهایی نمی‌تواند پاسخ‌گوی نیازهای پیچیده‌ی سیستم‌های هوشمند باشد. اینجاست که یادگیری نیمه‌نظارت‌شده (Semi-Supervised Learning) به‌عنوان یک راه‌حل میانی و هوشمندانه مطرح می‌شود.

یادگیری نیمه‌نظارت‌شده با ترکیب داده‌های برچسب‌دار محدود و حجم عظیمی از داده‌های بدون برچسب، تلاش می‌کند از هر دو جهان بهترین بهره را ببرد: دقت روش‌های نظارت‌شده و قدرت کشف الگوهای پنهان در روش‌های نظارت‌نشده. این رویکرد به مدل‌ها اجازه می‌دهد ساختار واقعی داده‌ها را بهتر درک کنند و مرزهای تصمیم‌گیری معنادارتری بسازند.

در این مقاله، مفهوم یادگیری نیمه‌نظارت‌شده، منطق و فرضیات زیربنایی آن، نحوه عملکرد، تفاوت آن با سایر روش‌های یادگیری ماشین و کاربردهای مهم آن در دنیای واقعی بررسی می‌شود .

تعریف

یادگیری نیمه‌نظارت‌شده شاخه‌ای از یادگیری ماشین است که با ترکیبی هوشمندانه از رویکردهای نظارت‌شده و نظارت‌نشده عمل می‌کند. این روش از هر دو نوع داده‌های برچسب‌دار و بدون برچسب استفاده می‌کند تا مدل‌های هوش مصنوعی را برای وظایف طبقه‌بندی و رگرسیون آموزش دهد.

اگرچه یادگیری نیمه‌نظارت‌شده معمولاً برای همان موارد کاربردی استفاده می‌شود که در روش‌های نظارت‌شده می‌بینیم. اما تمایز اصلی آن در تکنیک‌های متنوعی است که داده‌های بدون برچسب را نیز در کنار داده‌های برچسب‌دار (که لازمه‌ی روش‌های مرسوم هستند) وارد فرآیند آموزش می‌کند.

چالش‌های برچسب‌گذاری

برچسب‌گذاری صحیح داده‌ها برای وظایف پیچیدهٔ هوش مصنوعی، نیازمند تلاش و زمان قابل‌توجهی است.

• مثال ساده: برای آموزش مدلی که تفاوت بین ماشین و موتورسیکلت را بفهمد، صدها (یا هزاران) تصویر باید با برچسب ساده‌ی ماشین یا موتور نشانه‌گذاری شوند.
• مثال پیچیده‌تر (بینایی ماشین): برای وظیفه تشخیص اشیاء ، انسان‌ها نه تنها باید بگویند چه چیزی در تصویر است، بلکه باید دقیقاً مشخص کنند هر شیء در کجای تصویر قرار دارد.
• مثال دقیق: برای وظیفهٔ بخش‌بندیِ تصویر (Image Segmentation)، برچسب‌ها باید مرزهای دقیقِ پیکسل‌به‌پیکسلِ بخش‌های مختلف را در هر تصویر مشخص کنند.
  

بنابراین، برچسب‌گذاری داده‌ها می‌تواند برای برخی موارد بسیار خسته‌کننده باشد. در موارد تخصصی‌تر مانند کشف دارو، توالی‌یابی ژنتیکی یا طبقه‌بندی پروتئین، حاشیه‌نویسی داده‌ها نه تنها زمان‌بر است، بلکه نیازمند تخصص دامنه بسیار خاص و گران‌قیمت است.

Semi-Supervised Learning راهی ارائه می‌دهد تا بیشترین بهره را از مقدار اندکِ داده‌های برچسب‌دار ببریم، در حالی که همزمان از دریای وسیع داده‌های بدون برچسب نیز استفاده می‌کنیم.

یادگیری نیمه‌نظارت‌شده چگونه کار می‌کند؟

یادگیری نیمه‌نظارت‌شده (SSL) بر مجموعه‌ای از فرضیات کلیدی استوار است؛ از جمله اینکه داده‌های بدون برچسب ساختار منسجمی دارند و روابط معناداری میان نمونه‌های کلاس‌های مختلف وجود دارد. به عبارت دیگر، این روش «جادو» نیست؛ بلکه مبتنی بر اصول ریاضی و آماری مشخصی عمل می‌کند. در صورت نقض این اصول، انتظار بهبود عملکرد مدل بی‌جا خواهد بود.

شرط حیاتی: ارتباط و سنخیت داده‌ها

یک شرط ضروری برای یادگیری نیمه‌نظارت‌شده این است که نمونه‌های بدون برچسبی که برای آموزش استفاده می‌شوند، باید با وظیفه‌ای که مدل برای انجام آن آموزش می‌بیند، مرتبط (Relevant) باشند.

به بیان رسمی‌تر و ریاضیاتی:

توزیع داده‌های ورودی p(x) باید حاوی اطلاعاتی درباره توزیع پسین p(y|x) باشد.

به زبان ساده: توزیع احتمالی داده‌ها باید سرنخی دربارهٔ احتمال تعلّق هر دادهٔ (x) به یک کلاس خاص (y) به ما بدهد.

💡 مثال کاربردی (گربه و سگ):

فرض کنید می‌خواهید از داده‌های بدون برچسب کمک بگیرید تا یک طبقه‌بند تصویر را برای تشخیص تفاوت عکس‌های گربه و سگ آموزش دهید.

• دادهٔ مفید: مجموعهٔ دادهٔ آموزشی باید شامل تصاویر بدون برچسبی از گربه‌ها و سگ‌ها باشد.
• دادهٔ نامرتبط: افزودن تصاویر اسب‌ها و موتورسیکلت‌ها نه‌تنها فایده‌ای ندارد، بلکه مدل را گمراه می‌کند. چراکه توزیع آماری این داده‌ها با توزیع مورد نظر وظیفه هم‌خوانی ندارد.
  

فرضیاتِ بنیادی یادگیری نیمه‌نظارت‌شده

شرط اینکه توزیع داده‌ها  p(x) رابطه معناداری با کلاس‌ها  p(x|y)  داشته باشد، منجر به شکل‌گیری چندین فرضیه درباره ماهیت این رابطه می‌شود.

این فرضیات، موتور محرکِ اکثر (اگر نگوییم همه) روش‌های SSL هستند. به طور کلی، هر الگوریتم یادگیری نیمه‌نظارت‌شده تنها زمانی درست کار می‌کند که یک یا چند مورد از این فرضیات به صراحت یا به صورت ضمنی در داده‌ها صدق کنند.

۱. فرضیه خوشه (Cluster Assumption)

فرضیه خوشه بیان می‌کند که نقاط داده‌ای که متعلق به یک خوشه یکسان هستند (یعنی مجموعه‌ای از نقاط که شباهتشان به یکدیگر بیشتر از شباهتشان به سایر داده‌های موجود است)، به احتمال زیاد به یک کلاس واحد تعلق دارند.

اگرچه گاهی این فرضیه را به عنوان یک اصل مستقل در نظر می‌گیرند، اما ون انگل (Van Engelen) و هوس (Hoos) آن را این‌گونه توصیف کرده‌اند: تعمیمی از سایر فرضیات.

از این دیدگاه، تعیین اینکه چه چیزی یک خوشه را تشکیل می‌دهد، بستگی به این دارد که از چه تعریفی برای شباهت استفاده می‌کنیم:

• فرضیه همواری (Smoothness)
• فرضیه چگالی پایین (Low-density)
• فرضیه منیفولد (Manifold)

هرکدام از این‌ها صرفاً تعریف متفاوتی از اینکه چه چیزی دو نقطهٔ داده را شبیه به هم می‌کند، ارائه می‌دهند.

💡 مثال (دسته‌بندی اخبار): تصور کنید مجموعه‌ای از مقالات خبری دارید.

• الگوریتم خوشه‌بندی، مقالاتی که کلمات “فوتبال”، “لیگ برتر” و “گل” دارند را در یک گروه (خوشه) قرار می‌دهد.
• اگر شما فقط یک مقاله در این خوشه را با عنوان “اخبار ورزشی” برچسب‌گذاری کنید،
• طبق فرضیه خوشه، مدل فرض می‌کند که تمام مقالات دیگر در آن خوشه نیز “اخبار ورزشی” هستند.

۲. فرضیه همواری (Smoothness Assumption)

فرضیه همواری (که به نام فرضیه پیوستگی یا Continuity نیز شناخته می‌شود) بیان می‌کند که اگر دو نقطه داده، مثلاً x و x’، در فضای ورودی به هم نزدیک باشند، آنگاه برچسب‌های آن‌ها (y و y’) نیز باید یکسان باشند.

این فرضیه در اکثر روش‌های یادگیری نظارت‌شده مشترک است. برای مثال، طبقه‌بندها در طول آموزش یک تقریب معنادار از هر کلاس یاد می‌گیرند و پس از آموزش، داده‌های جدید را بر اساس اینکه به کدام‌یک از این تقریب‌ها شبیه‌تر (نزدیک‌تر) هستند، طبقه‌بندی می‌کنند.

جادوی انتقال‌پذیری (Transitivity) در SSL

در زمینه یادگیری نیمه‌نظارت‌شده (SSL)، فرضیه همواری یک مزیت فوق‌العاده دارد: قابلیت اعمال به صورت تراگذر (Transitive) روی داده‌های بدون برچسب.

بیایید یک سناریو با سه نقطه داده را تصور کنیم :

1. یک نقطه داده برچسب‌دار (x₁).
2. یک نقطه داده بدون برچسب (x₂) که به  x₁ نزدیک است.
3. یک نقطه داده بدون برچسب دیگر (x₃) که به x₂ نزدیک است، اما از x₁ دور است.

نتیجه‌گیری منطقی:

فرضیه همواری به ما می‌گوید که x₂ باید برچسبی مشابه x₁ داشته باشد (چون به هم نزدیک‌اند). همچنین می‌گوید x₃ باید برچسبی مشابه x₂ داشته باشد.

بنابراین، ما می‌توانیم فرض کنیم که هر سه نقطه داده دارای برچسب یکسانی هستند. چرا؟ زیرا برچسب x₁ به دلیل نزدیکی x₃ به x₂، به صورت زنجیره‌ای (تراگذر) به x₃ منتقل شده است، حتی اگر x₃ و x₁ مستقیماً کنار هم نباشند.

💡 مثال زنجیره دوستی:

• x₁ (علی): می‌دانیم طرفدار تیم “آبی” است (داده برچسب‌دار).
• x₂ (رضا): دوست صمیمی علی است (نزدیک به x₁). پس احتمالاً او هم طرفدار “آبی” است.
• x₃ (پژمان): دوست صمیمی رضا است (نزدیک به x₂)، اما علی را نمی‌شناسد (دور از x₁).
• نتیجه: طبق خاصیت تراگذر، سیستم نتیجه می‌گیرد پژمان هم طرفدار “آبی” است، چون این ویژگی از علی به رضا و از رضا به پژمان منتقل شده است.

۳. فرضیه چگالی پایین (Low-density Assumption)

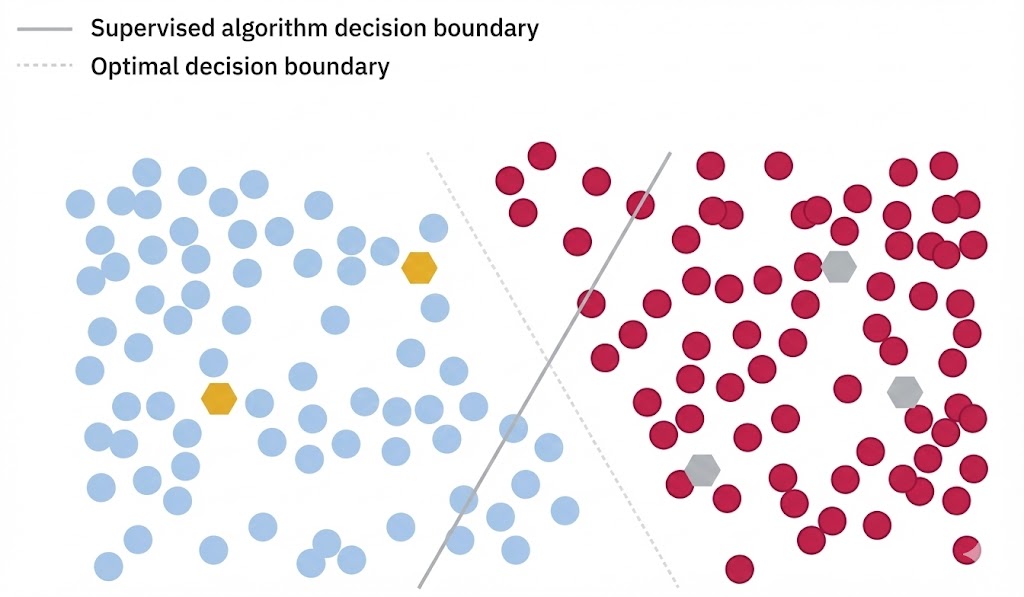
فرضیه چگالی پایین یک اصل ساده اما قدرتمند را بیان می‌کند: مرز تصمیم‌گیری (Decision Boundary) بین کلاس‌ها نباید از وسطِ نواحی پرچگالی و شلوغ عبور کند. به بیان دیگر، خطی که دسته‌ها را از هم جدا می‌کند، باید از منطقه‌ای بگذرد که نقاط داده‌ی کمی در آن وجود دارد (یک فضای خالی).

امتداد منطقی سایر فرضیات

فرضیه چگالی پایین را می‌توان به عنوان مکمل و امتداد دو فرضیه قبلی در نظر گرفت:

1. ارتباط با فرضیه خوشه: یک خوشه متراکم از نقاط، نشان‌دهنده یک کلاس است، نه مرز بین کلاس‌ها.
2. ارتباط با فرضیه همواری: اگر چندین نقطه داده نزدیک هم باشند، باید برچسب یکسانی داشته باشند. بنابراین، همه آن‌ها باید در یک طرف مرز تصمیم‌گیری قرار بگیرند (نه اینکه مرز از بین آن‌ها رد شود).

چرا این فرضیه مهم است؟

این نمودار نشان می‌دهد که ترکیب فرضیهٔ همواری (Smoothness Assumption) و فرضیهٔ جدایی در نواحی کم‌تراکم (Low-Density Separation) چگونه می‌تواند به ایجاد مرز تصمیم‌گیری‌ای شهودی‌تر و دقیق‌تر منجر شود. در حالتی که فقط از داده‌های برچسب‌دار استفاده شود، سیستم مجبور است بر اساس تعداد محدودی نمونه، مرزی تعریف کند — که ممکن است به‌اشتباه از میان خوشه‌های داده عبور کند. در مقابل، حضور داده‌های بدون برچسب، ساختار توزیع را آشکار می‌سازد و امکان قرار دادن مرز تصمیم در دره بین خوشه‌ها (یعنی ناحیه کم‌تراکم) را فراهم می‌آورد.

۴. فرضیه منیفولد (Manifold Assumption)

فرضیه منیفولد یک مفهوم هندسی عمیق اما بسیار کاربردی است. این فرضیه بیان می‌کند که:

فضای ورودی با ابعاد بالا (که بسیار پیچیده به نظر می‌رسد)، در واقع از چندین منیفولد با ابعاد پایین‌تر تشکیل شده است که تمام نقاط داده روی آن‌ها قرار دارند. نکته کلیدی اینجاست که نقاط داده‌ای که روی یک منیفولد مشترک قرار دارند، برچسب یکسانی دارند.

مثال : کاغذ مچاله شده

برای درک بهتر، یک تکه کاغذ را تصور کنید که مچاله شده و به شکل یک توپ درآمده است.

1. حالت مچاله (ابعاد بالا): مکان هر نقطه روی این سطح کروی و مچاله، نیازمند مختصات سه‌بعدی (x, y, z) است. در این حالت، ممکن است دو نقطه در فضا کنار هم باشند، در حالی که روی کاغذ کیلومترها از هم دورند (فقط چون کاغذ تا خورده و آن‌ها کنار هم قرار گرفته‌اند).
2. حالت صاف (منیفولد اصلی): اگر آن توپ مچاله را باز کنید و دوباره صاف کنید، همان نقاط را می‌توان تنها با مختصات دوبعدی  (x, y) نشان داد.

به این فرآیند کاهش ابعاد (Dimensionality Reduction) می‌گویند. در دنیای ریاضیات و یادگیری ماشین، این کار با روش‌هایی مانند خودکدگذارها (Autoencoders) یا لایه‌های کانولوشنی (Convolutions) انجام می‌شود تا ساختار اصلی و ساده داده از دل پیچیدگی ظاهری بیرون کشیده شود.

ابعاد در یادگیری ماشین: نفرین ابعاد

در یادگیری ماشین، بعد به معنای ابعاد فیزیکی نیست، بلکه به هر ویژگی یا صفت داده اشاره دارد.

💡 مثال فنی (تصاویر):

یک تصویر کوچک رنگی با اندازه ۳۲×۳۲ پیکسل را در نظر بگیرید.

• این تصویر ۱۰۲۴ پیکسل دارد.
• هر پیکسل ۳ مقدار رنگی (قرمز، سبز، آبی) دارد.
• بنابراین، این تصویر ساده دارای ۳,۰۷۲ بُعد است!

مقایسه نقاط داده در فضایی با این تعداد ابعاد بسیار دشوار است؛ هم به دلیل پیچیدگی محاسباتی و هم به این دلیل که بخش بزرگی از این فضای چند هزار بعدی، حاوی اطلاعات مفیدی نیست (نویز یا فضای خالی است).

نتیجه‌گیری فرضیه

فرضیه منیفولد بیان می‌کند که هنگامی مدل یاد می‌گیرد اطلاعات غیرضروری را حذف کند (یعنی کاهش ابعاد را انجام دهد) و داده‌ها را به منیفولد ذاتی‌شان نگاشت کند، نقاط دادهٔ پراکنده به نمایشی معنادارتر همگرا می‌شوند.

در این فضای جدید و ساده‌سازی‌شده، سایر فرضیات یادگیری نیمه‌نظارت‌شده — از جمله فرضیهٔ همواری و فرضیهٔ خوشه‌ای — با قابلیت اطمینان بالاتری عمل کرده و امکان کشف الگوهای پنهان فراهم می‌شود.

نگاشت و بازگشت: رازِ مرزهای دقیق

نگاشت نقاط داده به یک منیفولد با ابعاد پایین‌تر، می‌تواند یک مرز تصمیم‌گیری بسیار دقیق‌تر را فراهم کند؛ مرزی که سپس می‌توان آن را دوباره به فضای با ابعاد بالاتر ترجمه کرد (بازگرداند).

یادگیری فعال (Active Learning)

الگوریتم‌های یادگیری فعال رویکرد متفاوتی دارند؛ آن‌ها داده‌های بدون برچسب را به صورت خودکار برچسب‌گذاری نمی‌کنند. در عوض، آن‌ها در محیط‌های نیمه‌نظارت‌شده (SSL) به عنوان یک مشاور هوشمند عمل می‌کنند تا تعیین کنند کدام نمونه‌های بدون برچسب، اگر به صورت دستی برچسب‌گذاری شوند، مفیدترین و ارزشمندترین اطلاعات را به مدل می‌دهند.

به عبارت دیگر، مدل به جای اینکه کورکورانه هر داده‌ای را مصرف کند، داده‌ها را گلچین می‌کند و فقط در مورد موارد دشوار یا مبهم از انسان کمک می‌خواهد.

نتایج امیدوارکننده

استفاده از یادگیری فعال در تنظیمات نیمه‌نظارت‌شده نتایج بسیار نویدبخشی داشته است. یک مطالعه اخیر نشان داد که استفاده از این روش در وظیفه پیچیده‌ قطعه‌بندی معنایی ، مقدار داده‌های برچسب‌دار مورد نیاز برای آموزش موثر مدل را به کمتر از نصف کاهش داده است. این یعنی صرفه‌جویی عظیم در زمان و هزینه متخصصان.

مثال کاربردی (تشخیص تومور در پزشکی): فرض کنید یک رادیولوژیست می‌خواهد به هوش مصنوعی آموزش دهد تا تومورها را در عکس‌های MRI تشخیص دهد.

• روش سنتی: رادیولوژیست باید ۱۰۰۰ عکس تصادفی را بررسی و برچسب‌گذاری کند (که بسیاری از آن‌ها عکس‌های سالم و ساده هستند و اطلاعات جدیدی به مدل نمی‌دهند).
• با یادگیری فعال: مدل ابتدا خودش عکس‌ها را می‌بیند. عکس‌های واضح (کاملاً سالم یا کاملاً بیمار) را کنار می‌گذارد. سپس ۱۰۰ عکس مشکوک و پیچیده را که در تشخیص آن‌ها شک دارد، جدا کرده و به رادیولوژیست نشان می‌دهد: لطفا فقط این‌ها را برایم برچسب بزن.
• نتیجه: مدل با دیدن این ۱۰۰ نمونه‌ی سخت، همان‌قدر یاد می‌گیرد که با دیدن آن ۱۰۰۰ عکس یاد می‌گرفت، اما با ۱۰٪ زحمت برای پزشک.

یادگیری نیمه‌نظارت‌شده در برابر نظارت‌شده و نظارت‌نشده

یادگیری نیمه‌نظارت‌شده را می‌توان به عنوان یک ترکیب (Hybrid) یا حد وسط بین یادگیری نظارت‌شده و نظارت‌نشده در نظر گرفت.

مقایسه: یادگیری نیمه‌نظارت‌شده در برابر نظارت‌شده

تمایز اصلی میان یادگیری ماشین نیمه‌نظارت‌شده و تمام‌نظارت‌شده در نوع داده‌های آموزشی است:

• یادگیری نظارت‌شده: تنها با استفاده از مجموعه داده‌های کاملاً برچسب‌دار آموزش می‌بیند.
• یادگیری نیمه‌ نظارت‌شده: ترکیبی از نمونه‌های داده برچسب‌دار و بدون برچسب در فرآیند آموزش استفاده می‌کند.

مفهوم یادگیرنده پایه: تکنیک‌های نیمه‌نظارت‌شده، یک الگوریتم نظارت‌شده (که در این زمینه به آن یادگیرنده پایه می‌گویند) را اصلاح یا تکمیل می‌کنند تا بتواند اطلاعاتِ نمونه‌های بدون برچسب را نیز جذب کند. در این روش، نقاط داده‌ی برچسب‌دار برای پایه‌ریزی پیش‌بینی‌های مدل و افزودن ساختار به مسئله (مثلاً اینکه چند کلاس وجود دارد و ویژگی‌های اصلی هر کدام چیست) استفاده می‌شوند.

هدف: مرز تصمیم‌گیری دقیق هدف در آموزش هر مدل طبقه‌بندی، یادگیری یک مرز تصمیم‌گیری دقیق است: خطی (یا در داده‌های با بیش از دو بُعد، یک ابرصفحه) که نقاط داده‌ی یک دسته را از نقاط داده‌ی دسته دیگر جدا می‌کند.

اگرچه یک مدل تمام‌نظارت‌شده هم می‌تواند از نظر فنی تنها با استفاده از چند نقطه داده‌ی برچسب‌دار، یک مرز تصمیم‌گیری یاد بگیرد، اما مشکل اینجاست که چنین مدلی ممکن است روی مثال‌های دنیای واقعی به خوبی تعمیم پیدا نکند (Generalize) و پیش‌بینی‌های غیرقابل‌اعتمادی ارائه دهد.

مثال کلاسیک:

مجموعه داده نیمه‌ماه‌ها (Half-moons) این مجموعه داده، نقص‌های مدل‌های نظارت‌شده‌ای را که به داده‌های برچسب‌دار متکی هستند، به وضوح نشان می‌دهد.

• سناریو: اگرچه مرز تصمیم‌گیری صحیح باید دو شکل هلالی (نیمه‌ماه) را از هم جدا کند، یک مدل نظارت‌شده احتمالاً دچار بیش‌برازش (Overfit) می‌شود؛ یعنی فقط همان چند نقطه برچسب‌دار را یاد می‌گیرد و شکل کلی هلال‌ها را نادیده می‌گیرد.
• مزیت نیمه‌نظارت‌شده: نقاط داده‌ی بدون برچسب به وضوح زمینه (Context) و شکلِ ساختاری داده‌ها را منتقل می‌کنند، اما یک الگوریتم نظارت‌شده سنتی نمی‌تواند این داده‌های بدون برچسب را پردازش کند و در نتیجه کورکورانه عمل می‌کند.

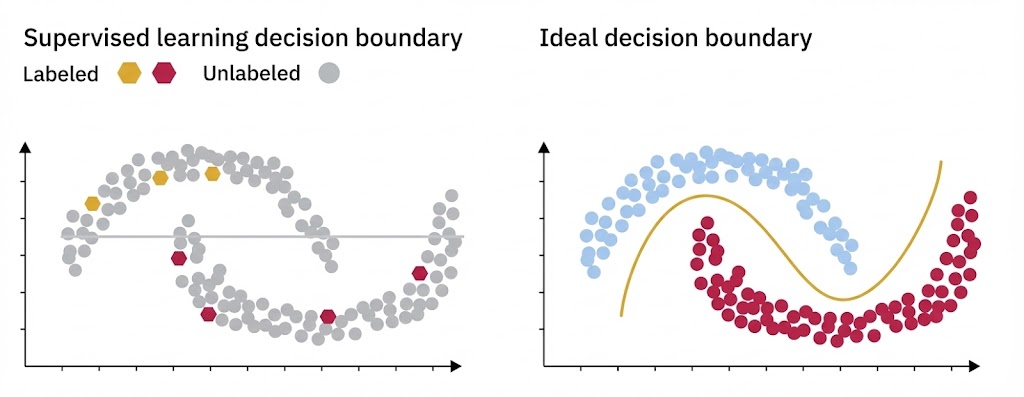
محدودیت‌های مدل نظارت‌شده و تفاوت با نظارت‌نشده

استفاده از تنها تعداد محدودی نقطه (داده برچسب‌دار) در مدل‌های نظارت‌شده، مانند رانندگی در شب با چراغ‌های خاموش است. در این حالت، مدل ممکن است یک مرز تصمیم‌گیری (Decision Boundary) یاد بگیرد که تعمیم‌پذیری ضعیفی دارد و در مواجهه با نمونه‌های جدید، مستعد خطاهای فاحش در طبقه‌بندی باشد.

یادگیری نیمه‌نظارت‌شده در برابر نظارت‌نشده

۱. فقدان حقیقت مبنا در نظارت‌نشده

برخلاف یادگیری نیمه‌نظارت‌شده، الگوریتم‌های یادگیری نظارت‌نشده از هیچ داده برچسب‌دار یا تابع زیانی استفاده نمی‌کنند.

• تفاوت کلیدی: یادگیری نظارت‌نشده از هرگونه زمینه یاحقیقت مبنا که بتوان با آن دقت مدل را سنجید و بهینه کرد، دوری می‌کند.

۲. رویکرد مدرن: از پیش‌آموزش تا تنظیم دقیق (LLMs)

یک رویکرد نیمه‌نظارت‌شده که روز به روز رایج‌تر می‌شود (به‌ویژه در مدل‌های زبانی بزرگ یا LLMها)، فرآیند دومرحله‌ای زیر است:

1. پیش‌آموزش (Pre-training): مدل ابتدا از طریق وظایف نظارت‌نشده آموزش می‌بیند تا نمایش‌های معناداری از مجموعه داده‌های عظیم و بدون برچسب یاد بگیرد.
2. یادگیری خودنظارت‌شده (Self-supervised): وقتی این وظایف شامل یک حقیقت مبنا و تابع زیان باشند (اما بدون دخالت و حاشیه‌نویسی دستی انسان)، به آن یادگیری خودنظارت‌شده می‌گویند.
3. تنظیم دقیق: پس از مرحله اول، مدل با مقدار کمی داده برچسب‌دار تنظیم می‌شود.

• نتیجه: این مدل‌های پیش‌آموزش‌دیده اغلب می‌توانند عملکردی قابل رقابت با مدل‌های تمام‌نظارت‌شده داشته باشند.

۳. شکست خوشه‌بندی در برابر اشکال پیچیده

اگرچه روش‌های نظارت‌نشده مفید هستند، اما فقدان زمینه (Context) باعث می‌شود که به تنهایی برای وظایف طبقه‌بندی مناسب نباشند. بیایید دوباره به مثال مجموعه داده نیمه‌ماه‌ها نگاه کنیم:

• چالش: یک الگوریتم خوشه‌بندی معمولی )مثل K-Means) داده‌ها را بر اساس نزدیکی فیزیکی به مرکز خوشه گروه‌بندی می‌کند.
• شکست: چنین الگوریتمی احتمالاً دو شکل هلالی را از وسط نصف می‌کند (یک دایره دورِ نیمه بالایی و یک دایره دور نیمه پایینی می‌کشد)، چون نمی‌تواند مفهوم شکلِ خمیده را بدون داشتنِ چند نمونه برچسب‌دار درک کند.

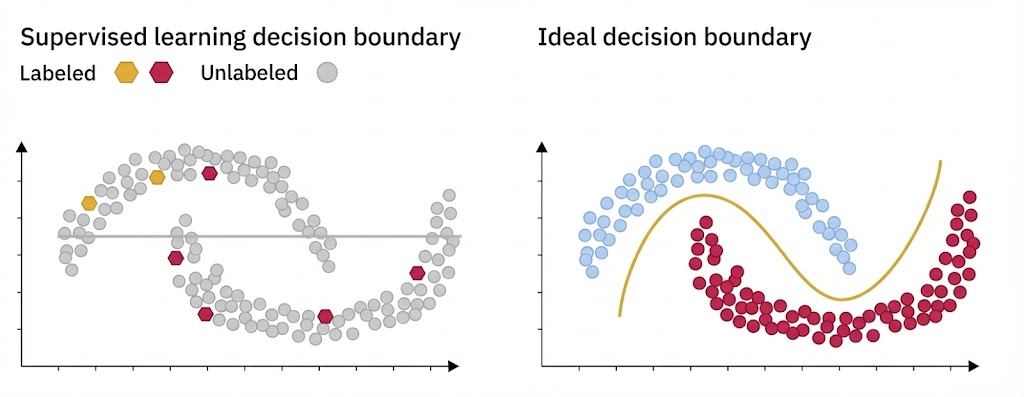
یادگیری نیمه‌نظارت‌شده در برابر یادگیری خودنظارت‌شده

هر دو یادگیری نیمه‌نظارت‌شده و خودنظارت‌شده با هدفی مشترک طراحی شده‌اند: کاهش وابستگی به حجم زیادی از داده‌های برچسب‌دار. با این حال، در نحوهٔ دستیابی به این هدف، تفاوتی بنیادین دارند.

۱. تفاوت در مواد اولیه

• یادگیری نیمه‌نظارت‌شده: این روش همچنان به مجموعه‌ای کوچک از داده‌های برچسب‌دار نیاز دارد تا جهت یادگیری را برای مدل مشخص کند.
  
• یادگیری خودنظارت‌شده: این روش (مانند خودکدگذارها یا Autoencoders) واقعاً ماهیت نظارت‌نشده دارد و در مرحله اول نیازی به معلم خارجی ندارد.

۲. منبع حقیقت (Ground Truth) از کجاست؟

در حالی که یادگیری نظارت‌شده (و نیمه‌نظارت‌شده) به یک حقیقت مبنای خارجی نیاز دارد (همان برچسب‌هایی که انسان‌ها می‌زنند)، یادگیری خودنظارت‌شده، حقیقت را از ساختار درونی خودِ داده‌های خام بیرون می‌کشد.

۳. وظایف بهانه‌ای (Pretext Tasks)

بسیاری از کارهایی که مدل در یادگیری خودنظارت‌شده انجام می‌دهد، به خودی خود هدف نهایی نیستند. ارزش آن‌ها در این است که به مدل یاد می‌دهند داده‌ها را بفهمد تا بعداً در مراحل بعدی (Downstream Tasks) بتواند کارهای اصلی را انجام دهد. به همین دلیل، به این مراحل اولیه، وظایف بهانه‌ای می‌گویند.

💡 مثال فنی (مدل زبانی): مدل زبانی ابتدا یاد می‌گیرد جاهای خالی یک جمله را پر کند (وظیفه بهانه‌ای). هدف ما پر کردن جای خالی نیست؛ هدف این است که مدل دستور زبان و معنی کلمات را بفهمد تا بعداً بتوانیم از آن بخواهیم یک مقاله کامل بنویسد یا ترجمه کند (وظیفه اصلی).

۴. ترکیب نهایی

زمانی که وظایف خودنظارتی (pretext tasks) با وظایف نظارت‌شدهٔ پایین‌دستی ترکیب شوند، بخشی از یک فرآیند یادگیری نیمه‌نظارت‌شدهٔ بزرگ‌تر را تشکیل می‌دهند: روشی که در نهایت از داده‌های برچسب‌دار و بدون برچسب به‌طور یکپارچه برای آموزش مدل استفاده می‌کند.

مزایا و محدودیت‌های یادگیری نیمه‌نظارت‌شده

یادگیری نیمه‌نظارت‌شده (SSL) ابزاری قدرتمند است، اما کارایی آن مستلزم شناخت عمیق از محدودیت‌ها و قابلیت‌های ذاتی آن است.

مزایا

۱. ناجیِ کلاس‌های کمیاب: در حالت عادی، اگر یک کلاس نمونه‌های کمی داشته باشد، مدل آن را نادیده می‌گیرد. SSL با استفاده از داده‌های بدون برچسب، نمونه‌های بیشتری از این کلاس‌های کمیاب پیدا کرده و یادگیری برای این گروه‌های زیرمجموعه را تقویت می‌کند.

۲. مقرون‌به‌صرفه و اقتصادی: بزرگترین مزیت تجاری آن؛ با بهره‌گیری هوشمندانه از داده‌های بدون برچسب (که رایگان و فراوان هستند)، وابستگی به برچسب‌گذاری دستیِ گران‌قیمت و زمان‌بر را به شدت کاهش می‌دهد.

۳. انعطاف‌پذیر و مستحکم : این مدل‌ها مانند خودروهای همه‌جارو (All-terrain) هستند؛ می‌توانند انواع مختلف داده‌ها و منابع را مدیریت کنند و خود را با تغییرات توزیع داده‌ها در طول زمان وفق دهند.

۴. خوشه‌بندی بهبودیافته:  داده‌های بدون برچسب به مدل کمک می‌کنند تا مرزهای بین گروه‌ها را شفاف‌تر ببیند. این باعث می‌شود خوشه‌ها دقیق‌تر تعریف شوند و تفکیک کلاس‌ها با کیفیت بالاتری انجام شود.

محدودیت‌ها

۱. پیچیدگی مدل: این روش بزن و برو (Plug-and-play) نیست. انتخاب معماری مناسب و تنظیم دقیق فراپارامترها نیازمند تخصص بالا و تنظیمات گسترده است تا مدل درست کار کند.

۲. خطر داده‌های نویزی: داده‌های بدون برچسب کنترل نشده هستند و ممکن است حاوی خطا یا اطلاعات نامربوط باشند. اگر مدل این نویزها را به عنوان الگو یاد بگیرد، عملکردش به شدت افت می‌کند (پدیده “Garbage in, Garbage out” در اینجا تشدید می‌شود).

۳. چالش در ارزیابی: چطور می‌توان به مدلی نمره داد وقتی پاسخ‌نامه کامل را نداریم؟ به دلیل محدود بودن داده‌های برچسب‌دار و کیفیت متغیر داده‌های بدون برچسب، سنجش دقیق عملکرد مدل و اطمینان از صحت آن دشوار است.

نتیجه گیری

یادگیری نیمه‌نظارت‌شده پلی میان یادگیری نظارت‌شده و نظارت‌نشده است که با بهره‌گیری هم‌زمان از داده‌های برچسب‌دار و بدون برچسب، امکان آموزش مدل‌هایی دقیق‌تر، منعطف‌تر و مقرون‌به‌صرفه‌تر را فراهم می‌کند. این روش با تکیه بر فرضیاتی مانند خوشه‌بندی، همواری، چگالی پایین و منیفولد، به مدل کمک می‌کند ساختار درونی داده‌ها را بشناسد و از این شناخت برای بهبود تعمیم‌پذیری استفاده کند.

اگرچه یادگیری نیمه‌نظارت‌شده با چالش‌هایی همراه است—از جمله وابستگی به صحت فرضیات، حساسیت به نویز داده‌ها و دشواری در ارزیابی عملکرد—اما پژوهشگران آن را در کاربردهای گسترده‌ای، از بینایی ماشین و پردازش زبان طبیعی تا پزشکی و سیستم‌های توصیه‌گر، راهکاری کارآمد و اقتصادی می‌دانند.

هنگامی که داده‌های برچسب‌دار از نظر حجم محدود، اما داده خام فراوان در دسترس باشند، یادگیری نیمه‌نظارت‌شده به‌عنوان راهکاری بهینه مطرح می‌شود. این چارچوب با کاهش چشمگیر نیاز به برچسب‌گذاری انسانی، امکان توسعهٔ مدل‌هایی با عملکرد بالا و مقیاس‌پذیری گسترده را فراهم می‌کند.