KModes چیست؟
KModes یک الگوریتم خوشهبندی است که در علم داده برای گروهبندی نقاط داده مشابه به خوشهها بر اساس ویژگیهای دستهبندی آنها استفاده میشود. برخلاف الگوریتمهای خوشهبندی سنتی که از معیارهای فاصله استفاده میکنند، KModes با شناسایی حالتها یا مقادیر متداول در هر خوشه برای تعیین مرکز آن کار میکند. KModes برای خوشه بندی داده های طبقه بندی شده مانند جمعیت شناسی مشتری، بخش های بازار یا پاسخ های نظرسنجی ایده آل است. این ابزار قدرتمندی برای تحلیلگران داده و دانشمندان است تا بینش خود را در مورد داده های خود به دست آورند و تصمیمات آگاهانه بگیرند.
خوشهبندی K-mode یک تکنیک یادگیری ماشینی بدون نظارت است که برای گروهبندی مجموعهای از اشیاء داده در تعداد مشخصی از خوشهها، بر اساس ویژگیهای دستهبندی آنها استفاده میشود. این الگوریتم “K-Mode” نامیده می شود زیرا از حالت ها (یعنی متداول ترین مقادیر) به جای میانگین یا میانه ها برای نشان دادن خوشه ها استفاده می کند.
در K-means خوشهبندی زمانی است که از دادههای دستهبندی پس از تبدیل آن به شکل عددی استفاده میکنیم. برای داده های با ابعاد بالا نتیجه خوبی نمی دهد.
بنابراین، برخی تغییرات برای داده های طبقه بندی t ایجاد شده است.
فاصله اقلیدسی را با متریک عدم تشابه جایگزین کنید
میانگین را با حالت برای مراکز خوشه جایگزین کنید.
یک روش مبتنی بر فرکانس را در هر تکرار برای به روز رسانی حالت اعمال کنید.
و سپس به دلیل حالت MODE به این حالت K-MODE Clustering می گویند.
KModes vs KMeans
KMeans از معیارهای ریاضی (فاصله) برای خوشه بندی داده های پیوسته استفاده می کند. هر چه فاصله کمتر باشد، نقاط داده ما شبیهتر هستند. Centroids توسط Means به روز می شوند. اما برای نقاط داده طبقهای، ما نمیتوانیم فاصله را محاسبه کنیم. بنابراین به سراغ الگوریتم KModes می رویم. از تفاوتها (تناسب کلی) بین نقاط داده استفاده میکند. هرچه تفاوتها کمتر باشد، نقاط داده ما شبیهتر هستند. از حالت ها به جای وسایل استفاده می کند.
الگوریتم KModes چگونه کار می کند؟
برخلاف روشهای خوشهبندی سلسله مراتبی، باید K را از قبل مشخص کنیم.
- K مشاهدات را به صورت تصادفی انتخاب کنید و از آنها به عنوان رهبر/خوشه استفاده کنید
- تفاوت ها را محاسبه کنید و هر مشاهده را به نزدیکترین خوشه خود اختصاص دهید
- حالت های جدیدی را برای خوشه ها تعریف کنید
- 2 تا 3 مرحله را تکرار کنید تا زمانی که نیازی به تخصیص مجدد نباشد
امیدوارم تاکنون ایده اولیه الگوریتم KModes را دریافت کرده باشید. بنابراین اجازه دهید به سرعت مثالی بزنیم تا گام به گام کار را نشان دهیم.
نحوه عملکرد خوشه بندی K-Modes:
اجازه دهید X مجموعه ای از اشیاء داده های طبقه بندی شده باشد
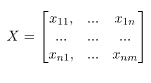
که میتوان آنرا نشان داد
و حالت Z بردار است
سپس، به حداقل رساندن
معادله متریک عدم تشابه را برای اشیاء داده اعمال کنید
فرض کنید میخواهیم K خوشه کنیم، سپس Q = [q_{k1},q_{k1},….,q_{km}] \epsilon Q داریم
وظیفه اصلی الگوریتم K-Modes به حداقل رساندن تابع هزینه C(Q) است.
از مراحل زیر تشکیل شده است.
- K شی داده را برای هر خوشه انتخاب کنید.
2. تفاوت ها را محاسبه کنید و هر شی داده را به نزدیکترین خوشه اختصاص دهید.
3. حالت های جدید را برای همه خوشه ها محاسبه کنید.
4.مراحل 2 و 3 را تکرار کنید تا خوشه پایدار شود.
برخی از تغییرات الگوریتم K-modes ممکن است از روشهای مختلفی برای بهروزرسانی مرکزها (حالتهای) خوشهها استفاده کنند، مانند گرفتن حالت وزنی یا میانه اشیاء درون هر خوشه.
به طور کلی، هدف از خوشهبندی K-modes به حداقل رساندن تفاوتهای بین اشیاء داده و مرکز (حالتها) خوشهها، با استفاده از معیار تشابه طبقهای مانند فاصله همینگ است.
مثال
تصور کنید مجموعه داده ای داریم که اطلاعاتی در مورد رنگ مو، رنگ چشم و رنگ پوست افراد دارد. هدف ما این است که آنها را بر اساس اطلاعات موجود گروه بندی کنیم (شاید بخواهیم ایده هایی برای طراحی پیشنهاد دهیم)
رنگ مو، رنگ چشم و رنگ پوست همه متغیرهای دسته بندی هستند. در زیر نشان داده شده است که چگونه مجموعه داده ما به نظر می رسد.
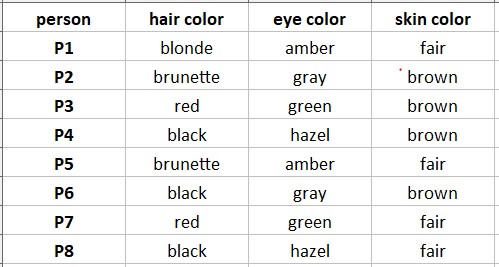
بسیار خوب، ما اکنون داده های نمونه را داریم. اجازه دهید با تعریف تعداد خوشه ها (K)=3 ادامه دهیم
مرحله 1: K مشاهدات را به صورت تصادفی انتخاب کنید و از آنها به عنوان رهبر/خوشه استفاده کنید
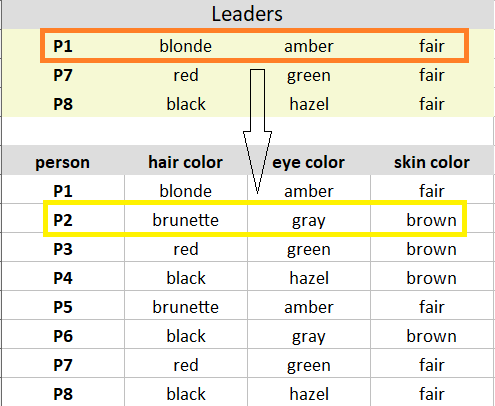
من P1، P7، P8 را به عنوان رهبران/خوشه ها انتخاب می کنم
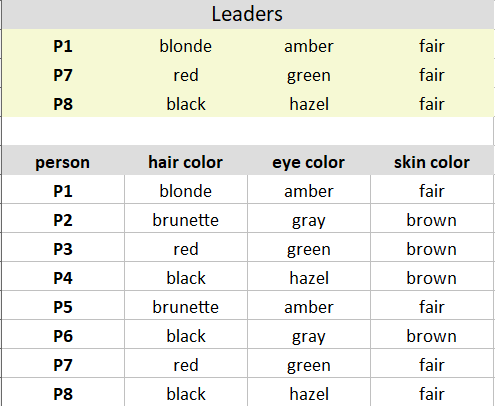
مرحله 2: عدم شباهت ها (تعداد عدم تطابق) را محاسبه کنید و هر مشاهده را به نزدیکترین خوشه خود اختصاص دهید.
به طور مکرر نقاط داده های خوشه ای را با هر یک از مشاهدات مقایسه کنید. نقاط داده مشابه 0 و نقاط داده غیرمشابه 1 می دهند.
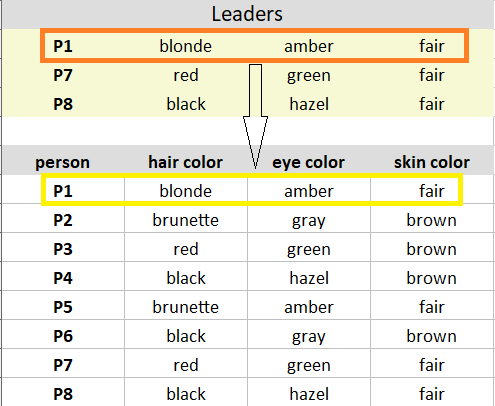
مقایسه رهبر/خوشه P1 با مشاهده P1 0 عدم شباهت به دست می دهد.
مقایسه رهبر/خوشه P1 با مشاهده P2 3 (1+1+1) تفاوت را به دست می دهد.
به همین ترتیب، تمام تفاوتها را محاسبه کرده و مطابق شکل زیر در یک ماتریس قرار دهید و مشاهدات را به نزدیکترین خوشه آنها (خوشهای که کمترین تفاوت را دارد) اختصاص دهید.
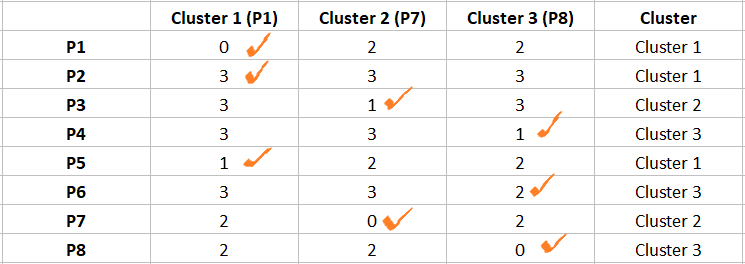
پس از مرحله 2، مشاهدات P1، P2، P5 به خوشه 1 اختصاص داده می شود. P3، P7 به خوشه 2 اختصاص داده می شوند. و P4، P6، P8 به خوشه 3 اختصاص داده شده اند.
توجه: اگر همه خوشه ها با یک مشاهده تفاوت مشابهی دارند، به هر خوشه به طور تصادفی اختصاص دهید. در مورد ما، مشاهده P2 دارای 3 تفاوت با همه رهبران است. من به طور تصادفی آن را به خوشه 1 اختصاص دادم.
مرحله 3: حالت های جدیدی را برای خوشه ها تعریف کنید
حالت به سادگی بیشترین مقدار مشاهده شده است.
مشاهدات را با توجه به خوشه ای که به آن تعلق دارند علامت گذاری کنید. مشاهدات خوشه 1 با رنگ زرد، خوشه 2 با قرمز آجری و خوشه 3 با بنفش مشخص شده اند.
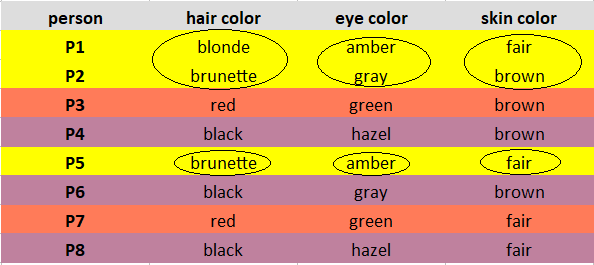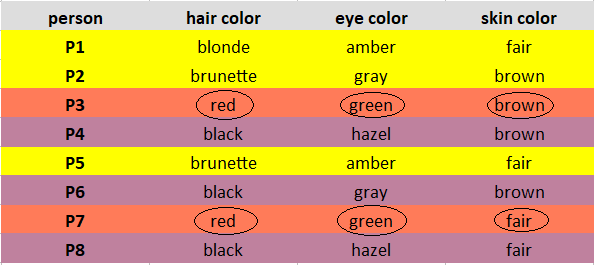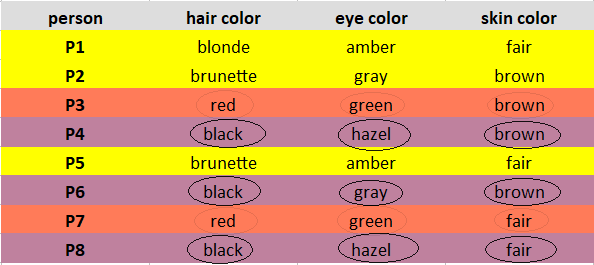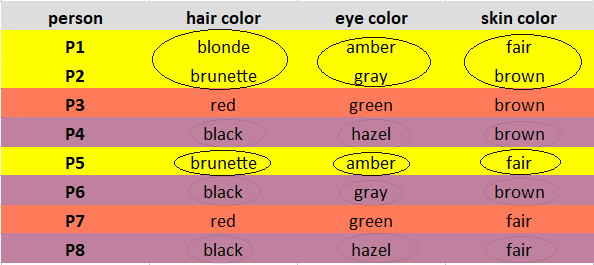
با در نظر گرفتن یک خوشه در یک زمان، برای هر ویژگی، به دنبال Mode باشید و رهبران جدید را به روز کنید.
توضیح: مشاهدات خوشه 1 (P1, P2, P5) دارای رنگ موی سبزه به عنوان بیشترین مشاهده شده، کهربایی به عنوان بیشترین مشاهده رنگ چشم و روشن به عنوان بیشترین مشاهده رنگ پوست است.
توجه: اگر مقادیر مشابهی را مشاهده کردید، حالت را به طور تصادفی انتخاب کنید. در مورد ما، مشاهدات خوشه 3 (P3، P7) دارای یک رنگ پوست قهوه ای و روشن است. من به طور تصادفی رنگ قهوه ای را به عنوان حالت انتخاب کردم.
در زیر رهبران جدید ما پس از به روز رسانی هستند.
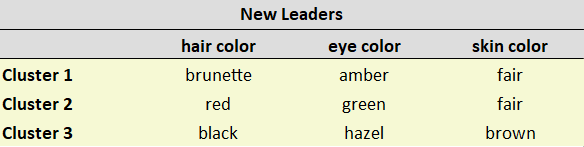
مراحل 2-4 را تکرار کنید
پس از به دست آوردن رهبران جدید، مجدداً تفاوت های بین مشاهدات و رهبران تازه به دست آمده را محاسبه کنید.
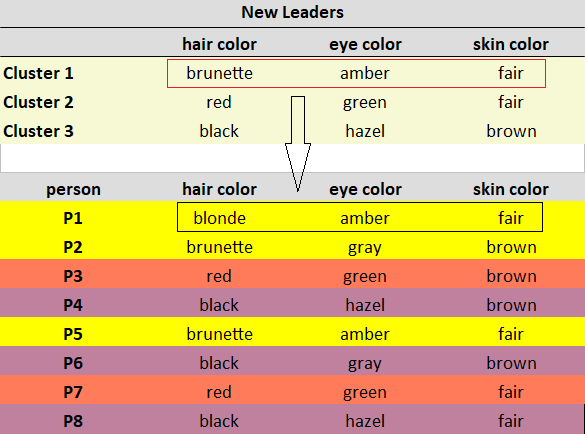
مقایسه خوشه 1 با مشاهده P1 1 عدم شباهت به دست می دهد.
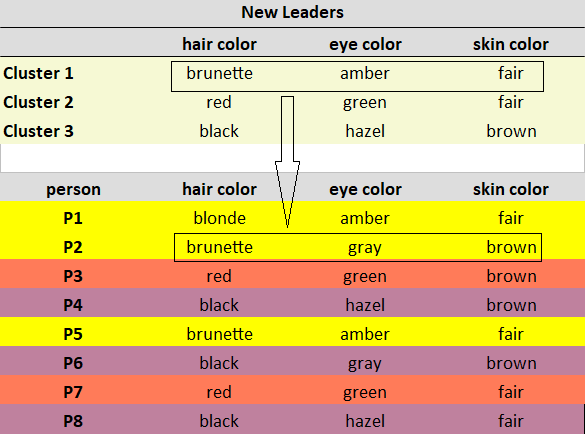
مقایسه خوشه 1 با مشاهده P2 2 عدم شباهت به دست می دهد.
به همین ترتیب، تمام تفاوت ها را محاسبه کرده و در یک ماتریس قرار دهید. هر مشاهده را به نزدیکترین خوشه خود اختصاص دهید.
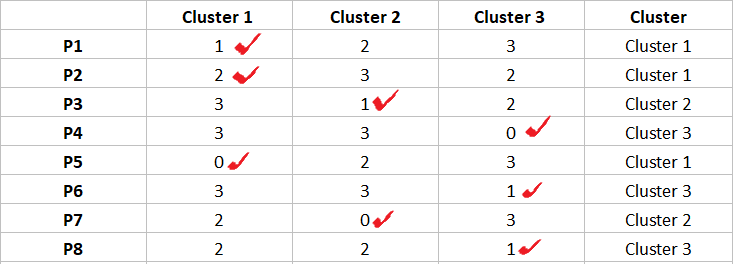
مشاهدات P1، P2، P5 به خوشه 1 اختصاص داده شده است. P3، P7 به خوشه 2 اختصاص داده می شوند. و P4، P6، P8 به خوشه 3 اختصاص داده شده اند.
ما در اینجا توقف می کنیم زیرا می بینیم که هیچ تغییری در تعیین تکلیف مشاهدات وجود ندارد.
اندازه گیری عدم تشابه بین دو شی داده
K-modes الگوریتمی برای خوشه بندی داده های طبقه بندی شده است. برای تقسیم یک مجموعه داده به تعداد مشخصی از خوشهها استفاده میشود، جایی که هر خوشه با یک حالت مشخص میشود که متداولترین مقدار طبقهبندی در خوشه است.
اندازه گیری شباهت و عدم تشابه برای تعیین فاصله بین اشیاء داده در مجموعه داده استفاده می شود. در مورد K-mode، این فواصل با استفاده از یک اندازه گیری عدم تشابه به نام فاصله هامینگ محاسبه می شوند. فاصله هامینگ بین دو شی داده، تعداد صفات طبقه بندی شده ای است که بین دو شیء متفاوت است.
اجازه دهید x و y دو شی داده طبقه بندی شده باشند که توسط m ویژگی ها یا ویژگی ها تعریف می شوند.
جایی که،
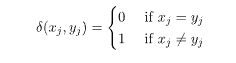
Python Example
Implementation of KModes in Python
Begin with Importing necessary libraries
# importing necessary libraries
import pandas as pd
import numpy as np
# !pip install kmodes
from kmodes.kmodes import KModes
import matplotlib.pyplot as plt
%matplotlib inline
Creating Toy Dataset
Scree Plot or Elbow Curve to Find Optimal Kvalue
برای KModes، هزینه را برای محدوده ای از مقادیر K ترسیم کنید. هزینه مجموع تمام تفاوتهای بین خوشهها است.
در جایی که یک خم آرنج مانند با ارزش هزینه کمتر را مشاهده می کنید، K را انتخاب کنید.
# Elbow curve to find optimal K
cost = []
K = range(1,5)
for num_clusters in list(K):
kmode = KModes(n_clusters=num_clusters, init = "random", n_init = 5, verbose=1)
kmode.fit_predict(data)
cost.append(kmode.cost_)
plt.plot(K, cost, 'bx-')
plt.xlabel('No. of clusters')
plt.ylabel('Cost')
plt.title('Elbow Method For Optimal k')
plt.show()
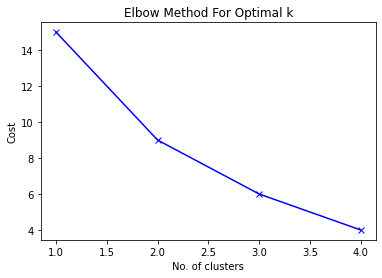
ما می توانیم خمشی را در K=3 در نمودار بالا ببینیم که نشان می دهد 3 تعداد بهینه خوشه ها است.
Build a Model with 3 Clusters
# Building the model with 3 clusters
kmode = KModes(n_clusters=3, init = "random", n_init = 5, verbose=1)
clusters = kmode.fit_predict(data)
clusters
Finally, insert the predicted cluster values in our original dataset.
data.insert(0, "Cluster", clusters, True)
data
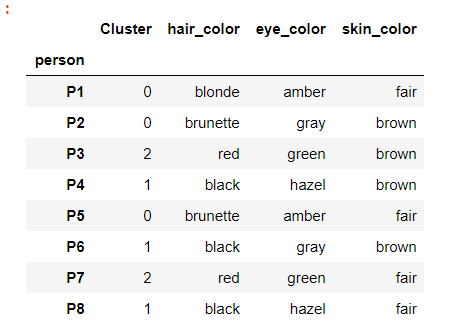
استنتاج از پیشبینیهای مدل: P1، P2، P5 به عنوان یک خوشه ادغام میشوند. P3، P7 ادغام شدند. و P4، P6، P8 ادغام می شوند.
نتایج رویکرد نظری ما با پیشبینیهای مدل مطابقت دارد.




