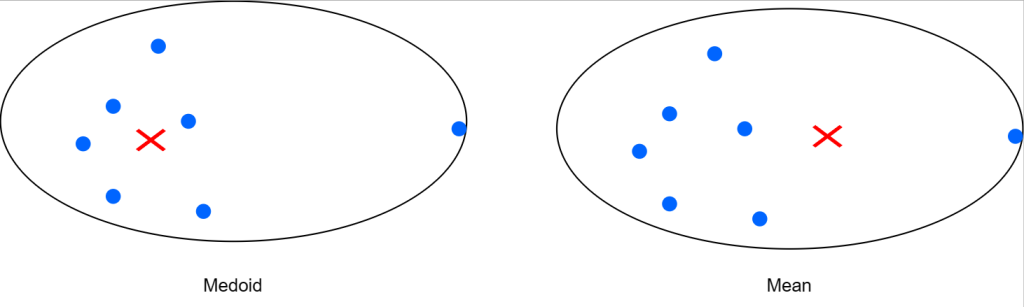
در الگوریتم k-means ابتدا میانگین داده های داخل یک خوشه را محاسبه می کردیم و به عنوان مرکز خوشه قرار میدادیم و فاصله ی تمام نقاط تا تا مرکز سه خوشه بدست میاوردم . در الگوریتم k-mediods نیازی به محاسبه ی مرکز خوشه نیست در این الگوریتم یکی از دادههای داخل خوشه را به صورت تصادفی انتخاب میکنیم فاصله ی تمام نقاط تا نقطه ی انتخابی را محاسبه میکنیم . K-means زمانی مناسب است که بتوانیم با فواصل اقلیدسی کار کنیم
الگوریتم های خوشه بندی k-mediods :
- PAM (تقسیم بندی در اطراف خوشه بندی)
- CLARA (خوشه بندی برنامه های کاربردی بزرگ)
- CLARANS (خوشه بندی تصادفی برنامه های کاربردی بزرگ)

مزایای الگوریتم
مزایای الگوریتم k-mediods:
- درک آن ساده است و اسان برای پیاده سازی.
- الگوریتم K-Medoid سریع است و در تعداد ثابتی از مراحل همگرا می شود.
- PAM نسبت به سایر الگوریتم های پارتیشن بندی نسبت به سایر الگوریتم های پارتیشن بندی کمتر حساس است.
معایب الگوریتم
- عیب اصلی الگوریتم K-Medoid این است که برای خوشه بندی گروه های غیر کروی (دلخواه شکل) اشیاء مناسب نیست. این به این دلیل است که به حداقل رساندن فاصله بین اشیاء غیر medoid و medoid (مرکز خوشه) متکی است – به طور خلاصه، از فشرده سازی به عنوان معیارهای خوشه بندی به جای اتصال استفاده می کند.
- ممکن است نتایج مختلفی را برای اجراهای مختلف در همان مجموعه داده به دست اورد، زیرا اولین k medoids به طور تصادفی انتخاب می شوند.
مراحل پیاده سازی
مراحل پیاده سازی الگوریتم k-mediods :
- از بین نقاط k نقطه را به صورت تصادفی انتخاب کنید به عنوان mediods
- فاصله ی بین نقاط دیگر تا k نقطه را با استفاده از فاصله ی منهتن محاسبه کنید
- Manhattan Distance = | x1 – x2 | + | y1 –y2 |
- از بین فواصل بدیت آمده از هر mediods کمترین فواصل را انتخاب کنید و به mediods متناظر نسبت دهید
- کمترین فواصل انتخاب شده را باهم جمع بزنید
- مجدد یکسری نقاط دیگر به تعداد k به صورت رندوم برای mediods انتخاب کنید
- مراحل بالا را مجدد انجام دهید
- در نهایت حاصل جمع فواصل در سری اول را از حاصل جمع فواصل در سری دوم کم میکنیم و به یک عدد میرسید
- اگر عدد بالا بزرگتر از صفر باشد مبادله را متوقف کنید و نقاط k سری اول را به عنوان mediods انتخاب کنید و انتخاب k سری دوم کار نادرستی بوده است
مثالهای کاربردی
📌 مثال1
دو تکرار از الگوریتم خوشه بندی k-medoids را برای نقاط داده زیر نشان دهید.
فرض کنید k=2 و میانگین خوشه اولیه (1,1) باشد. (2،3).
پس از اولین تکرار، مدویدهای خوشه ای و پس از هر تکرار محتویات خوشههارا بدهید.
از متریک فاصله منهتن استفاده کنید.


2 nd Iteration
C1: 0,2 1,1 2,0 1,3 2,3
C2: 5,5 6,6 7,7
C2: 1,3 2,3 5,5 6,6 7,7
1,3: 0+1+6+8+10=25
2,3: 1+0+5+7+9=22
5,5: 8+6+5+0+2+4=17
6,6 :8+7+2+0+2=19
7,7: 10+9+4+2+0=24
M2:5,5
1 st Iteration:
C1: 0,2 1,1 2,0
0,2: 0+2+4=6
1,1: 2+0+2=4
2,0: 4+2+0=6
M1: 1,1
📌 مثال2

- مقداردهی اولیه: k نقطه تصادفی را از n نقطه داده به عنوان medoids انتخاب کنید.
- هر نقطه داده را با استفاده از هر روش متریک فاصله مشترک به نزدیکترین medoid مرتبط کنید.
- در حالی که هزینه کاهش می یابد: مبادله m و o، هر نقطه داده را به نزدیکترین medoid مرتبط می کند و هزینه را دوباره محاسبه می کند.
- اگر کل هزینه بیشتر از مرحله قبلی باشد، مبادله را خنثی کنید.
مرحله 1: اجازه دهید 2 مدوئید به طور تصادفی انتخاب شود، بنابراین k = 2 را انتخاب کنید و اجازه دهید C1 – (4، 5) و C2 – (8، 5) دو مدوئید باشند.
مرحله 2: محاسبه هزینه. ناهماهنگی هر نقطه غیر مدوئیدی با مدوئیدها محاسبه و جدولبندی میشود:

در اینجا از فرمول فاصله منهتن برای محاسبه ماتریس فاصله بین نقاط مدوئید و غیر مدوئید استفاده شده است. این فرمول می گوید که فاصله = |X1-X2 | + |Y1-Y2|. هر نقطه به خوشه ای از ان medoid اختصاص داده شده است که تفاوت کمتری دارد. نقاط 1، 2 و 5 به خوشه C1 و 0، 3، 6، 7، 8 به خوشه C2 می روند. هزینه = (3 + 4 + 4) + (3 + 1 + 1 + 2 + 2) = 20
مرحله 3: به طور تصادفی یک نقطه غیر medoid را انتخاب کنید و هزینه را دوباره محاسبه کنید. اجازه دهید نقطه به طور تصادفی انتخاب شده باشد (8، 4). تفاوت هر نقطه غیر medoid با medoids – C1 (4، 5) و C2 (8، 4) محاسبه و جدول بندی می شود.

هر نقطه به خوشه ای اختصاص داده می شود که تفاوت ان کمتر است. بنابراین، نقاط 1، 2 و 5 به خوشه C1 و 0، 3، 6، 7، 8 به خوشه C2 می روند. هزینه جدید = (3 + 4 + 4) + (2 + 2 + 1 + 3 + 3) = 22 هزینه مبادله = هزینه جدید – هزینه قبلی = 22 – 20 و 2 >0 از انجا که هزینه سواپ کمتر از صفر نیست، ما سواپ را خنثی می کنیم. از این رو (4، 5) و (8، 5) medoids نهایی هستند. خوشه بندی به روش زیر خواهد بود پیچیدگی زمان است.





