درک الگوریتم گرادیان کاهشی (Gradient Descent) و ریاضیات پشت آن

مقدمه

در دنیای یادگیری ماشین و یادگیری عمیق، آموزش یک مدل چیزی فراتر از اجرای چند خط کد است. سؤال اصلی همیشه این است:
چگونه مدل بفهمد در چه جهتی و با چه سرعتی باید پارامترهای خود را تغییر دهد تا به بهترین نتیجه برسد؟

پاسخ این سؤال در الگوریتمی نهفته است که ستون فقرات بهینه‌سازی در هوش مصنوعی محسوب می‌شود: الگوریتم گرادیان کاهشی (Gradient Descent). این الگوریتم به مدل کمک می‌کند تا با اصلاح تدریجی وزن‌ها، فاصله خود را از پاسخ مطلوب کاهش دهد و از دل خطاها، مسیر یادگیری را پیدا کند.

در این مقاله، گرادیان کاهشی را نه صرفاً به‌عنوان یک فرمول ریاضی، بلکه به‌عنوان یک فرآیند یادگیری هوشمند بررسی می‌کنیم. از تصویرسازی شهودی و مفاهیم پایه گرفته تا تحلیل ریاضی، انواع بهینه‌سازها، چالش‌های واقعی و پیاده‌سازی عملی با داده‌های واقعی، تلاش شده است این الگوریتم به شکلی عمیق، قابل فهم و کاربردی توضیح داده شود.

تعریف گرادیان کاهشی

الگوریتم گرادیان کاهشی (Gradient Descent) در واقع «نقشه راه» مدل برای یادگیری است. بیایید با یک مثال هیجان‌انگیز، منطق ریاضی این ابزار قدرتمند را از زاویه‌ای جدید ببینیم.

تصویرسازی: ماجراجویی در مه غلیظ

تصور کنید در قله یک کوه بلند ایستاده‌اید و مِهی غلیظ تمام فضا را پوشانده است؛ چشمان شما عملاً جایی را نمی‌بیند. هدف شما رسیدن به امن‌ترین و پایین‌ترین نقطه دره است، یعنی جایی که «خطا» به حداقل می‌رسد.

در این وضعیت، شما تنها یک ابزار دارید: احساس شیب زمین زیر پاهایتان.

معادل‌سازی دنیای واقعی با دنیای ریاضیات:

برای اینکه یک متخصص هوش مصنوعی باشید، باید بتوانید این سفر را به زبان ریاضی ترجمه کنید:

• کوهستان مه آلود: همان تابع زیان (Loss Function) یا کوه خطاهای ماست.
• برداشتن قدم‌ها: همان تغییرات کوچکی است که ما در وزن‌ها  ایجاد می‌کنیم تا مدل اصلاح شود.
• احساس شیب زمین: در ریاضیات به این حس، مشتق یا گرادیان می‌گوییم؛ یعنی جهتی که بیشترین کاهش خطا را به ما نشان می‌دهد.

.

فرآیند گام‌به‌گام: سقوط هوشمندانه از تپه خطا

برای اینکه در سریع‌ترین زمان ممکن به پایه تپه (نقطه بهینه) برسید، مدل شما یک چرخه تکرار شونده را دنبال می‌کند:

1. اسکن محیط: ابتدا در همان نقطه‌ای که هستید، تمام جهات را بررسی می‌کنید تا بفهمید “تندترین شیب به سمت پایین” کدام طرف است.
2. برداشتن گام استراتژیک: پس از یافتن جهت، یک «گام کوچک» و حساب‌شده برمی‌دارید. (یادمان باشد: گام‌های خیلی بزرگ در مه خطرناک است!) .
3. توقف و ارزیابی: در موقعیت جدید دوباره می‌ایستید و شیب را چک می‌کنید. شاید جهت دره کمی تغییر کرده باشد.
4. تکرار تا پیروزی: این فرآیند «جستجوی جهت» و «برداشتن گام» را آنقدر ادامه می‌دهید تا شیب زمین زیر پایتان صفر شود. اینجاست که شما به کمینه مطلق (Global Minimum) رسیده‌اید؛ یعنی دقیق‌ترین حالت ممکن برای مدل هوش مصنوعی شما.

.

گرادیان کاهشی (Gradient Descent)؛ از فرضیات آماری تا محاسبات شبکه‌های عصبی

الگوریتم گرادیان کاهشی، قلب تپنده بهینه‌سازی در یادگیری ماشین و شبکه‌های عصبی است. این الگوریتم یک حل‌کننده تکرار شونده (Iterative Solver) است که به ما می‌گوید وزن‌های مدل را چقدر و در چه جهتی تغییر دهیم تا تابع هدف (خطا) به حداقل برسد.

۱. شهود بصری: سفر به عمق دره خطا

برای درک بهتر، تصور کنید در بالای یک کوه (نقطه حداکثر خطا) هستید و می‌خواهید به پایین‌ترین نقطه دره (حداقل خطا) برسید، اما مه غلیظی مانع دید شماست. در این حالت، شما با پاهای خود شیب زمین را احساس کرده و در جهتی قدم برمی‌دارید که بیشترین شیب را به سمت پایین دارد.

• کوه: همان تابع زیان یا خطا (Loss Function) است.
• قدم‌ها: تغییراتی است که در وزن‌ها (W) ایجاد می‌کنیم.
• شیب: همان مشتق یا گرادیان تابع نسبت به وزن‌هاست.

.

۲. مفاهیم حیاتی در کنترل حرکت

برای رسیدن به نقطه بهینه، دو فاکتور کلیدی وجود دارد:

1. جهت حرکت(Direction): مشتق یا گرادیان در هر نقطه، شیب خط مماس را نشان داده و جهت پایین رفتن را مشخص می‌کند.
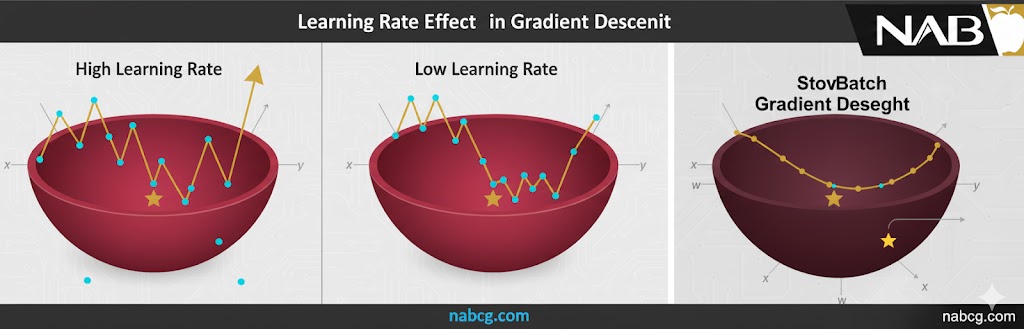
2. اندازه گام یا نرخ یادگیری(Learning Rate / α): ضریبی که تعیین می‌کند گام‌های ما به سمت پایین چقدر بزرگ یا کوچک باشند.
   •  α بالا: باعث سرعت می‌شود اما خطر رد شدن از نقطه بهینه (Overshooting) را دارد.
   • α پایین: دقت را بالا می‌برد اما به توان محاسباتی و تکرار بیشتری نیاز دارد.

۳. رگرسیون خطی؛ آزمایشگاهی برای درک هزینه

در یک مدل رگرسیون خطی با معادله Y = mX + b، هدف ما تنظیم وزن‌ها (m و b) به گونه‌ای است که مجموع فاصله بین خط پیش‌بینی و نقاط واقعی به حداقل برسد.

تفاوت فنی Loss و Cost:

• تابع زیان(Loss Function): خطا را فقط برای یک نمونه آموزشی محاسبه می‌کند.
• تابع هزینه(Cost Function): میانگین یا مجموع خطاها را در کل مجموعه داده می‌سنجد.

از نظر ریاضی، تابع هزینه در اینجا مشابه یک تابع سهمی (U شکل) است که یک مینیمم مطلق (Global Minimum) دارد و مدل با برداشتن گام‌های کوچک سعی می‌کند به پایین‌ترین نقطه آن برسد.

۴. استخراج ریاضی فرمول به‌روزرسانی (Update Rule)

برای اینکه مدل وزن‌ها را اصلاح کند، از دو قاعده اساسی در حساب دیفرانسیل استفاده می‌کنیم: قاعده توان (برای مشتق‌گیری از مربع خطا) و قاعده زنجیره‌ای (برای انتقال خطا از خروجی به لایه‌های عقب‌تر(.

فرمول کلی به‌روزرسانی:

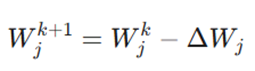
تحلیل اجزای فرمول:

• W_j^{k+1}: موقعیت بعدی یا وزن جدید در تکرار. k+1
• W_j^k: موقعیت فعلی یا وزن موجود در تکرار فعلی. k
• ΔW_j: مقدار تغییر، که همان شیب یا مشتق تابع نسبت به وزن است.

.

فرمول تفصیلی (عملیاتی):

در برنامه‌نویسی شبکه‌های عصبی برای محاسبه مقدار تغییر وزن استفاده می‌شود:

تشریح پارامترهای عملیاتی:

•  α (نرخ یادگیری): ضریبی که تعیین می‌کند قدم‌های ما به سمت پایین تپه چقدر بزرگ باشد.
•   Y ^- Y (مقدار خطا): تفاوت بین پیش‌بینی مدل (Y^) و مقدار واقعی هدف .(Y)
• X_j: مقدار ورودی مربوط به آن وزن خاص.
• Σ: مجموع خطاها برای تمام نمونه‌های آموزشی (رکوردهای مشتریان).

این فرمول قلب تپنده بخش انتشار رو به عقب (Backward Propagation) است. شبکه با محاسبه تفاوت پیش‌بینی (Y^) و واقعیت (Y)، متوجه می‌شود که هر وزن چقدر در ایجاد خطا نقش داشته است و آن را اصلاح می‌کند.

۵. استانداردسازی و مراحل نهایی

در دنیای شبکه‌های عصبی، پارامتر b (بایاس) را به عنوان  θ _0 و m (وزن) را به عنوان  θ _1 می‌شناسیم. فرآیند اصلاح به صورت گام‌به‌گام انجام می‌شود:

1. تغییر در شیب Error . X . Learning Rate: (Δm)
2. تغییر در عرض از مبدأ   Error . Learning Rate:(Δb)
3. به‌روزرسانی نهایی:

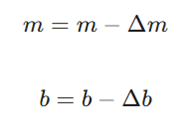
تعریف متغیرها:

• Δm: تغییرات کوچک در مقدار m (مشتق تابع هزینه نسبت به شیب).
• Δb: تغییرات کوچک در مقدار b (مشتق تابع هزینه نسبت به عرض از مبدأ).

این فرآیند تا زمان همگرایی (Convergence) ادامه می‌یابد؛ یعنی زمانی که تغییرات در تابع زیان بسیار ناچیز شده و مدل به بهینه‌ترین حالت خود برسد.

انواع گرادیان کاهشی

در دنیای یادگیری عمیق، همه‌ی راه‌ها به یک مقصد ختم می‌شوند: کمینه کردن خطا. اما سوال اینجاست که با چه استراتژی و سرعتی باید این مسیر را طی کرد؟ بر اساس ماهیت داده‌ها و توان محاسباتی، چندین روش برای اجرای الگوریتم گرادیان کاهشی وجود دارد که در ادامه هر کدام را از زوایای مختلف بررسی می‌کنیم.

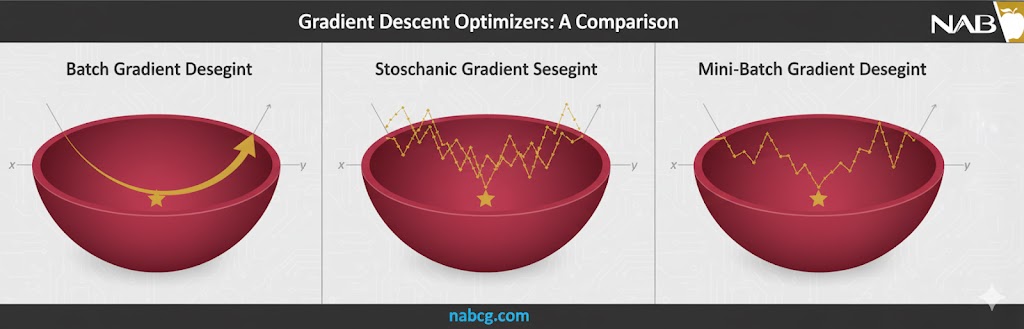
1. گرادیان کاهشی دسته‌ای(Batch Gradient Descent)
2. گرادیان کاهشی تصادفی(Stochastic Gradient Descent)
3. گرادیان کاهشی دسته‌ای کوچک(Mini-batch Gradient Descent)
4. گرادیان کاهشی مبتنی بر مومنتوم (Momentum-based)
5. الگوریتم آدگراد (Adagrad)
6. الگوریتم آر-ام-اس پراپ (RMSprop)
7. بهینه‌ساز آدام (Adam)

.

۱. گرادیان کاهشی دسته‌ای (Batch Gradient Descent)

این روش مانند یک مدیر وسواسی عمل می‌کند که تا تمام گزارش‌ها را نخواند، تصمیمی نمی‌گیرد. در این حالت، مدل خطای تمام نقاط داده در مجموعه آموزشی را جمع‌آوری کرده و تنها پس از بررسی کل داده‌ها، وزن‌ها را به‌روزرسانی می‌کند. به هر بار عبور کامل از کل مجموعه داده، یک اپوک (Epoch) گفته می‌شود.

• مزایا:
  • پایداری بالا: به دلیل میانگین‌گیری از تمام داده‌ها، نمودار تغییرات خطا بسیار نرم و پایدار است.
  • بهینگی در محاسبات: در مجموعه‌داده‌های کوچک، از نظر ریاضی بسیار کارآمد عمل می‌کند.
• معایب:
  • مصرف بالای حافظه: چون باید تمام داده‌ها را هم‌زمان در حافظه نگه دارد، برای داده‌های حجیم بسیار کُند و سنگین است.
  • خطر گیر افتادن: احتمال اینکه در یک کمینه محلی (Local Minimum) گیر بیفتد و هرگز به بهترین جواب (Global Minimum) نرسد، زیاد است.
• بهترین کاربرد: مجموعه‌داده‌های کوچک و زمانی که دقت و پایداری مسیر یادگیری اولویت اول باشد.

.

۲. گرادیان کاهشی تصادفی (Stochastic Gradient Descent – SGD)

اگر روش قبلی یک مدیر وسواسی بود، SGD مانند یک ورزشکار پرهیجان است! در این روش، مدل منتظر کل داده‌ها نمی‌ماند؛ بلکه بعد از دیدن هر یک دانه داده، بلافاصله وزن‌ها را اصلاح می‌کند.

• مزایا:
  • سرعت یادگیری: به دلیل به‌روزرسانی‌های مداوم، مدل خیلی سریع شروع به یادگیری می‌کند.
  • فرار از بن‌بست: نوسانات زیاد در مسیر حرکت باعث می‌شود مدل به راحتی از چاله‌های کمینه محلی خارج شده و شانس بیشتری برای یافتن کمینه مطلق داشته باشد.
  • کم‌حجم: فقط نیاز دارد یک نمونه داده را در حافظه نگه دارد.
• معایب:
  • مسیر نوسانی(Noisy): به دلیل تغییرات مکرر، مسیر حرکت به سمت هدف بسیار زیگزاگی و نامنظم است که ممکن است همگرایی نهایی را دشوار کند.
• بهترین کاربرد: مجموعه‌داده‌های بسیار بزرگ و آنلاین که داده‌ها به صورت جریانی (Stream) وارد می‌شوند.

.

۳. گرادیان کاهشی دسته‌ای کوچک (Mini-batch Gradient Descent)

این روش “نقطه تعادل” و محبوب‌ترین گزینه در دنیای واقعی است. مینی‌بچ، هوشمندیِ روش دسته‌ای را با سرعتِ روش تصادفی ترکیب می‌کند. در اینجا، داده‌ها به گروه‌های کوچکی (مثلاً ۳۲، ۶۴ یا ۱۲۸ تایی) تقسیم می‌شوند و به‌روزرسانی پس از بررسی هر گروه انجام می‌گیرد.

• مزایا:
  • بهترینِ هر دو دنیا: هم سرعت بالایی دارد و هم پایداری قابل قبولی در کاهش خطا از خود نشان می‌دهد.
  • بهینه‌سازی سخت‌افزاری: این روش به خوبی از قدرت پردازش موازی کارت‌های گرافیک (GPU) استفاده می‌کند.
• معایب:
  • نیاز به تنظیم: باید یک پارامتر اضافی به نام “Batch Size” را به صورت دستی تنظیم کنید که نیاز به تجربه دارد.
• بهترین کاربرد: تقریباً تمام پروژه‌های یادگیری عمیق مدرن و آموزش شبکه‌های عصبی پیچیده.

.

۴. گرادیان کاهشی مبتنی بر مومنتوم (Momentum-based)

این روش از قانون فیزیکی “تکانه” الهام گرفته است. در این حالت، مدل مانند یک توپ سنگین عمل می‌کند که وقتی از تپه به پایین می‌غلتد، سرعت گام‌های قبلی خود را حفظ کرده و با قدرت بیشتری به مسیر ادامه می‌دهد.

• مزایا: باعث سرعت بخشیدن به همگرایی می‌شود و به مدل کمک می‌کند تا به راحتی از روی نوسانات کوچک یا کمینه‌های محلی عبور کند.
• عملکرد: بخشی از جهت و سرعت حرکت قبلی را به آپدیت فعلی اضافه می‌کند تا در مسیرهای طولانی و تکراری، وقت تلف نشود.
• بهترین کاربرد: زمانی که مسیر تابع هزینه دارای نوسانات زیاد (شکلی شبیه به دره باریک) است.

.

۵. الگوریتم آدگراد (Adagrad)

آدگراد (Adaptive Gradient) یک بهینه‌ساز هوشمند است که بر اساس “تاریخچه” هر پارامتر تصمیم می‌گیرد. این الگوریتم نرخ یادگیری را برای هر پارامتر به صورت جداگانه تنظیم می‌کند.

• مزایا: برای داده‌های پراکنده (Sparse Data) فوق‌العاده است؛ زیرا به پارامترهایی که کمتر دیده شده‌اند، اجازه می‌دهد گام‌های بلندتری بردارند.
• معایب: از آنجایی که نرخ یادگیری مدام کاهش می‌یابد، ممکن است در مراحل نهایی آموزش، سرعت مدل به قدری کُند شود که دیگر چیزی یاد نگیرد.
• بهترین کاربرد: پردازش متن (NLP) و تحلیل داده‌هایی که برخی ویژگی‌های آن‌ها به ندرت ظاهر می‌شوند.

۶. الگوریتم آر-ام-اس پراپ (RMSprop)

این روش برای اصلاح مشکل بزرگ آدگراد (کُند شدن بیش از حد) معرفی شد. به جای نگاه کردن به کل تاریخچه، فقط به میانگین متحرک توان دوم گرادیان‌های اخیر نگاه می‌کند.

• مزایا: نرخ یادگیری را به شکلی متعادل تنظیم می‌کند تا آموزش مدل در مراحل پایانی متوقف نشود.
• عملکرد: مشابه آدگراد است اما با حافظه‌ای کوتاه‌مدت و هوشمندتر برای تعدیل نرخ یادگیری.
• بهترین کاربرد: آموزش شبکه‌های عصبی بازگشتی (RNN) و مسائل پیچیده یادگیری عمیق.

۷. بهینه‌ساز آدام (Adam)

آدام (Adaptive Moment Estimation) در حال حاضر پادشاه بهینه‌سازها در دنیای هوش مصنوعی است. این الگوریتم ترکیبی هوشمندانه از سه روش Momentum، Adagrad  و RMSprop است.

• مزایا: هم شتاب حرکت (Momentum) را دارد و هم نرخ یادگیری را به صورت خودکار برای هر پارامتر تنظیم می‌کند. (Adaptive Learning Rate)
• عملکرد: آدام میانگین متحرک گرادیان‌ها و توان دوم آن‌ها را به صورت همزمان محاسبه می‌کند تا دقیق‌ترین و سریع‌ترین مسیر را پیدا کند.
• بهترین کاربرد: تقریباً تمام مدل‌های مدرن هوش مصنوعی، از تشخیص تصویر تا چت‌بات‌های پیشرفته، از Adam استفاده می‌کنند.

.

جدول مقایسه هوشمندترین بهینه‌سازها

نام الگوریتم	ویژگی اصلی	سرعت همگرایی	نیاز به تنظیم دستی نرخ یادگیری
Momentum	استفاده از شتاب حرکت	بالا	بله
Adagrad	نرخ یادگیری اختصاصی برای هر پارامتر	متوسط	کم
RMSprop	جلوگیری از کُند شدن آموزش	بالا	کم
Adam	ترکیب شتاب و نرخ یادگیری تطبیقی	بسیار بالا	بسیار کم (خودکار)

چالش‌های جدی در مسیر گرادیان کاهشی

الگوریتم گرادیان کاهشی در مسائل محدب (Convex) به سادگی به هدف می‌رسد ؛ اما در مسائل غیرمحدب، با غول‌های زیر دست‌وپنجه نرم می‌کند:

۱. کمینه‌های محلی و نقاط زینی (Local Minima & Saddle Points)

زمانی که شیب تابع هزینه به صفر نزدیک می‌شود، مدل یادگیری را متوقف می‌کند. اما مشکل اینجاست که شیب صفر فقط مخصوص هدف نهایی (Global Minimum) نیست:

• کمینه محلی(Local Minima): نقاطی هستند که شبیه به هدف اصلی به نظر می‌رسند ؛ یعنی در هر دو طرف این نقطه، مقدار خطا افزایش می‌یابد، اما این بهترین جواب ممکن برای کل مدل نیست.
• نقاط زینی(Saddle Points): در این نقاط (که نامشان از زین اسب گرفته شده)، شیب فقط در یک جهت منفی است ؛ یعنی از یک سمت به ماکزیمم محلی و از سمت دیگر به مینیمم محلی می‌رسند.

نکته هوشمندانه: استفاده از گرادیان‌های پرنوسان (Noisy Gradients) که در روش‌هایی مثل SGD دیده می‌شود، می‌تواند به مدل کمک کند تا از این چاله‌ها فرار کرده و به سمت هدف اصلی حرکت کند.

۲. محو شدگی و انفجار گرادیان (Vanishing & Exploding Gradients)

در شبکه‌های عصبی عمیق (به‌ویژه RNNها)، زمانی که با استفاده از انتشار بازگشتی (Backpropagation) به عقب برمی‌گردیم، دو فاجعه ممکن است رخ دهد:

• محو شدگی گرادیان(Vanishing): زمانی رخ می‌دهد که گرادیان بیش از حد کوچک شود. با حرکت به سمت لایه‌های ابتدایی، این مقدار آنقدر کوچک می‌شود که به‌روزرسانی وزن‌ها عملاً متوقف شده (نزدیک به صفر) و لایه‌های اولیه شبکه دیگر چیزی یاد نمی‌گیرند.
• انفجار گرادیان(Exploding): دقیقاً برعکس حالت قبل؛ گرادیان بیش از حد بزرگ شده و باعث ناپایداری مدل می‌شود. در این حالت وزن‌ها به قدری بزرگ می‌شوند که به صورت NaN (عددی نیست) نمایش داده می‌شوند.

.

چه حوزه‌هایی از گرادیان کاهشی استفاده می‌کنند؟

الگوریتم گرادیان کاهشی در رشته‌های یادگیری ماشین  و یادگیری عمیق (Deep Learning) به کار گرفته می‌شود. یادگیری عمیق را می‌توان نسخه‌ای پیشرفته‌تر از یادگیری ماشین دانست که توانایی شناسایی ظریف‌ترین الگوها را دارد. پیاده‌سازی این الگوریتم‌ها معمولاً به دانش ریاضی و تسلط بر پایتون نیاز دارد.

۱. تحلیل داده‌های حجیم و پیش‌بینی روندها

یادگیری ماشین ابزاری حیاتی برای تحلیل دقیق و سریع حجم عظیمی از داده‌ها است. این علم به ما اجازه می‌دهد تا بر اساس رویدادها ووندهای گذشته، تحلیل‌های پیش‌بینانه انجام دهیم. به کمک هوش مصنوعی، می‌توان محدودیت‌های ذهن انسان در تحلیل جریان‌های بزرگ داده را پشت سر گذاشت و اجازه داد سیستم‌ها بدون دخالت مستقیم انسان، از داده‌های آنلاین بیاموزند.

۲. اینترنت اشیا (IoT) و خانه‌های هوشمند

یکی از کاربردهای جذاب گرادیان کاهشی در حوزه اشیاء متصل است. هوش مصنوعی با استفاده از این الگوریتم:

• خود را با عادات ساکنین یک خانه هوشمند تطبیق می‌دهد.
• دمای اتاق را بر اساس شرایط آب و هوایی تنظیم می‌کند.

.

۳. موتورهای جستجو و سیستم‌های پیشنهاددهنده

گرادیان کاهشی در قلب سیستم‌های غول‌آسایی همچون گوگل، یوتیوب، نتفلیکس و… قرار دارد. این الگوریتم‌ها با تحلیل داده‌های کاربران، علایق آن‌ها را درک کرده و نتایج جستجوی مرتبط یا پیشنهادهای خرید و تماشای فیلم را بهینه‌سازی می‌کنند.

۴. پردازش زبان طبیعی و دستیارهای صوتی

فناوری‌هایی که به کامپیوترها اجازه می‌دهند زبان انسان را درک و پردازش کنند، مدیون یادگیری ماشین هستند. دستیارهای دیجیتالی محبوبی مانند:

• Alexa
• Google Assistant
• Siri همگی از کاربردهای عملی گرادیان کاهشی برای فهم بهتر دستورات شما استفاده می‌کنند.

.

۵. بازی‌های ویدئویی و استراتژی‌های تجاری

توسعه‌دهندگان بازی‌های ویدئویی از این الگوریتم برای ساخت هوش مصنوعی‌های چالش‌برانگیز و واقع‌گرایانه استفاده می‌کنند. در دنیای تجارت نیز، هوش مصنوعی به شرکت‌ها کمک می‌کند تا نیازهای مشتریان و روندهای آینده بازار را پیش‌بینی کنند.

پیاده‌سازی گام‌به‌گام گرادیان کاهشی در پایتون

برای درک عمیق‌تر، ما از مجموعه‌داده واقعی Diabetes (دیابت) استفاده می‌کنیم تا رابطه بین شاخص توده بدنی (BMI) و پیشرفت بیماری را مدل‌سازی کنیم.

۱. فراخوانی کتابخانه‌های مورد نیاز

ابتدا کتابخانه‌های پایه مانند  NumPy برای محاسبات عددی،  Matplotlib برای رسم نمودارها و ابزارهای  Scikit-learn برای بارگذاری داده‌ها و استانداردسازی را وارد می‌کنیم.

۲. بارگذاری داده‌ها

مجموعه‌داده دیابت را بارگذاری کرده و ویژگی  BMI را به عنوان متغیر مستقل (X) و میزان پیشرفت بیماری را به عنوان هدف (y) انتخاب می‌کنیم.

۳. مقیاس‌دهی (Scaling) داده‌ها

از آنجایی که گرادیان کاهشی به مقیاس داده‌ها بسیار حساس است، از  StandardScaler استفاده می‌کنیم تا داده‌های BMI را نرمال‌سازی کنیم؛ این کار باعث همگرایی سریع‌تر و عملکرد بهتر الگوریتم می‌شود.

۴. مقداردهی اولیه پارامترها

پیش از شروع، پارامترهای مدل را تنظیم می‌کنیم:

• شیب (m) و عرض از مبدأ(c): هر دو را برابر با ۰ قرار می‌دهیم.
• نرخ یادگیری: مقدار ۰.۰۵ را انتخاب می‌کنیم.
• تعداد تکرار: الگوریتم را برای ۱۰۰۰ گام تنظیم می‌کنیم.

.

۵. اجرای حلقه اصلی گرادیان کاهشی

در هر تکرار از این حلقه، مراحل زیر انجام می‌شود:

• پیش‌بینی مقادیر: با استفاده از فرمول y_pred = m . X_scaled + c  حدس مدل محاسبه می‌شود.
• محاسبه خطا: تفاوت میان پیش‌بینی و واقعیت سنجیده شده و میانگین مربعات خطا (MSE) محاسبه می‌گردد.
• محاسبه گرادیان و به‌روزرسانی: مشتقات جزئی (dm و dc) محاسبه شده و مقادیر جدید  m و c  جایگزین می‌شوند.
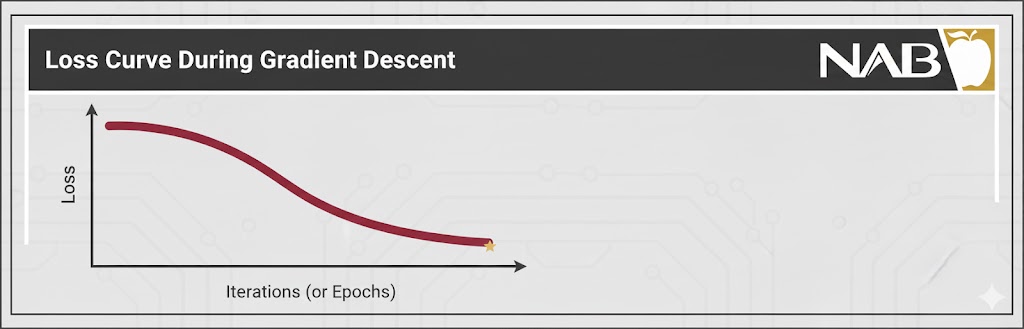
• ثبت تاریخچه زیان: مقدار Loss در هر مرحله ذخیره می‌شود تا روند کاهش خطا قابل مشاهده باشد.
• گزارش‌دهی: برای نظارت بر فرآیند یادگیری، وضعیت مدل هر ۱۰۰ تکرار یک‌بار چاپ می‌شود.

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_diabetes
from sklearn.preprocessing import StandardScaler

diabetes = load_diabetes()
X = diabetes.data[:, [2]]
y = diabetes.target
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
m, c = 0.0, 0.0
learning_rate = 0.05
iterations = 1000
loss_history = []

for i in range(iterations):
    y_pred = m * X_scaled.flatten() + c
    error = y_pred - y

    loss = np.mean(error ** 2)
    loss_history.append(loss)
    dm = (2 / len(X_scaled)) * np.dot(error, X_scaled.flatten())
    dc = (2 / len(X_scaled)) * np.sum(error)
    m -= learning_rate * dm
    c -= learning_rate * dc

    if i % 100 == 0:
        print(f"Iteration {i}: Loss={loss:.4f}, m={m:.4f}, c={c:.4f}")

print("\nFinal parameters:")
print(f"Slope (m): {m:.4f}, Intercept (c): {c:.4f}")

plt.scatter(X_scaled, y, alpha=0.5, label="Real Data")
plt.plot(X_scaled, m * X_scaled.flatten() + c,
         color='red', linewidth=2, label="Fitted Line")
plt.xlabel("BMI (scaled)")
plt.ylabel("Diabetes Progression")
plt.legend()
plt.show()

plt.plot(loss_history)
plt.xlabel("Iterations")
plt.ylabel("Loss (MSE)")
plt.title("Loss Curve on Diabetes Dataset")
plt.show()

خروجی:

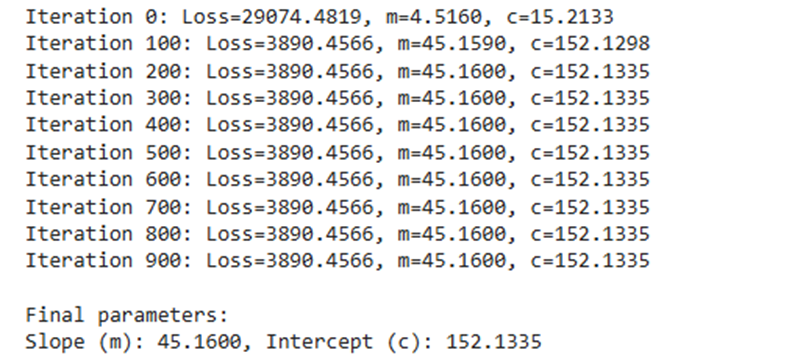
جمع بندی

الگوریتم گرادیان کاهشی قلب تپنده فرآیند یادگیری در یادگیری ماشین و شبکه‌های عصبی است. این الگوریتم با حرکت تدریجی در جهت کاهش تابع زیان، به مدل اجازه می‌دهد از اشتباهات خود بیاموزد و به‌مرور به پارامترهای بهینه نزدیک شود. بدون گرادیان کاهشی، آموزش مدل‌ها عملاً معنا و جهت مشخصی نخواهد داشت.

در این مقاله دیدیم که گرادیان کاهشی فقط یک روش واحد نیست، بلکه خانواده‌ای از استراتژی‌های بهینه‌سازی را شامل می‌شود؛ از روش‌های ساده‌ای مانند Batch و SGD گرفته تا بهینه‌سازهای پیشرفته‌ای مثل Momentum، RMSprop و Adam. هر یک از این روش‌ها با هدف بهبود سرعت همگرایی، پایداری یادگیری و عبور از چالش‌هایی مانند کمینه‌های محلی، نقاط زینی و ناپدید شدن گرادیان طراحی شده‌اند.

در نهایت، درک عمیق گرادیان کاهشی پلی میان ریاضیات، الگوریتم‌ها و یادگیری واقعی مدل‌ها ایجاد می‌کند. این الگوریتم پایه‌ی مفاهیمی مانند پس‌انتشار (Backpropagation) و آموزش شبکه‌های عصبی عمیق است و تسلط بر آن، شما را از استفاده‌کننده‌ی صرف مدل‌ها به یک طراح و تحلیل‌گر حرفه‌ای سیستم‌های هوشمند تبدیل می‌کند.