نوشته دکتر محمدرضا عاطفی

عضو هیات علمی دانشگاه
مشاور سازمانها و تحلیلگر سیستم
سری مدلسازی دینامیکی
مدل هموارسازی (مرتبه بالاتر)
Smooth (higher-order)
شرح مدل
یک هموارسازی مرتبه بالاتر، آبشاری از دو یا چند هموار است که در آن هر هموارسازی به هدف هموار بلافاصله پس از آن تبدیل میشود. موجودی هموار نهایی اغلب به عنوان متغیر “خروجی” در نظر گرفته میشود — این متغیری است که در نهایت به سمت هدف تنظیم میشود. حالت معمول این است که در هر مرحله هموارسازی کردن تاخیر یکسان باشد. یعنی اگر k ثابت باشد.

Order مرتبه تأخیر است
i هر مرحله خاص در آبشار است
k تأخیر برای هر مرحله جداگانه است و جایی
aggregateLag (یا میانگین تاخیر) به صورت زیر تعریف میشود

یا k به شکل زیر تعریف میشود:

به عنوان مثال در مورد بالا که در آن همه تاخیرها یکسان هستند، اگر مجموع تاخیر، مثلاً سی هفته باشد، پس تاخیر برای هر مرحله به شکل زیر خواهد بود:
 مورد استفاده:
مورد استفاده:
Hines cascaded coflow
کاربرد
چگونه میتوان یک «هموار» ایجاد کرد که در آن حرکت به سمت هدف به آرامی شروع میشود، سرعت میگیرد و سپس در مرحله نهایی کند میشود. چگونه میتوان سیستمی را مدلسازی کرد که در آن افراد در ابتدا تغییرات را دیر درک میکنند، اما در نهایت به طور کامل با ان منطبق میشوند.
مدل جریان و حالت:
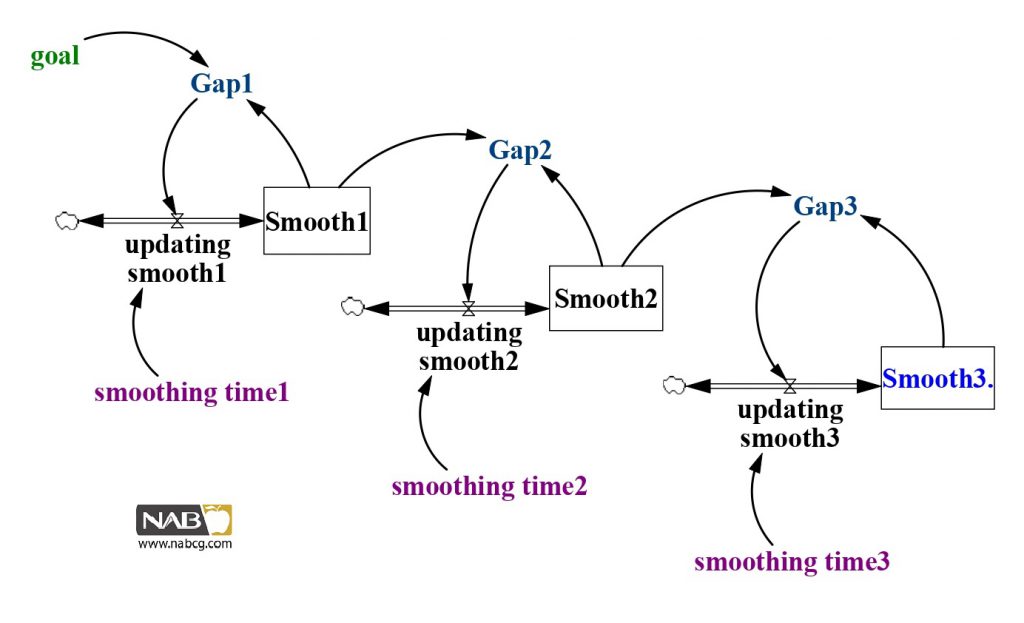
معادلات:
Smooth1 = INTEG( updating smooth1 , goal )
Units: stuff
updating smooth1 = Gap1 / smoothing time1
Units: stuff/Year
= smoothing time1
Units: Year
Gap1 = goal – Smooth1
Units: stuff
= goal
Units: stuff
Smooth2 = INTEG( updating smooth2 , Smooth1 )
Units: stuff
updating smooth2 = Gap2 / smoothing time2
Units: stuff/Year
= smoothing time2
Units: Year
Gap2 = Smooth1 – Smooth2
Units: stuff
“Smooth3.” = INTEG( updating smooth3 , Smooth2 )
Units: stuff
updating smooth3 = Gap3 / smoothing time3
Units: stuff/Year
smoothing time3 = 2
Units: Year
Gap3 = Smooth2 – “Smooth3.”
Units: stuff
رفتار:
در موردی که تاخیرهای هر مرحله همگی یکسان باشند، تعدیل ناگهانی تر و در نقطه تاخیر کل متمرکزتر میشود. تمام تعدیلها در مجموع تاخیر در صورت هموار بودن مرتبه نامتناهی اتفاق میافتد. (توجه داشته باشید که در چنین حالتی تاخیر کل یک عدد واقعی محدود و تاخیر هر مرحله بینهایت کوچک است و معادل :
 نمونههای کلاسیک:
نمونههای کلاسیک:
- هموارسازی کنندههای مرتبه سوم نسبتاً رایج هستند. هموارهای مرتبه دوم ، همانند هموارهای با مرتبه بالاتر از 3 بسیار نادر هستند.
توجه:
اگر تأخیرها را با تقسیم یک تاخیر کلی بر تعداد هموارها در آبشار ایجاد میکنید، مراقب خطای یکپارچه سازی باشید. به یاد داشته باشید که فاصله حل (“dt” یا “گام زمانی”) باید یک چهارم تا یک دهم کوچکترین ثابت زمانی باشد.
ثابت زمانی در یک هموارسازی مرتبه بالاتر تاخیر کلی نیست، بلکه تاخیر روی هموارهای هر مرحله است که آبشار را تشکیل میدهد. این ملاحظات حتی در هنگام استفاده از توابع هموارسازی مرتبه 3 ساخته شده توسط اکثر محیطهای مدل سازی شبیه سازی SD وجود دارد. این توابع داخلی معمولاً یک پارامتر برای تاخیر کلی میگیرند. به خاطر داشته باشید که در داخل نرم افزار این تاخیر کلی را به سه تاخیر جداگانه تبدیل میکند که هر یک به اندازه پارامتر “ثابت” زمان است.
نکات فنی:
اگر یک نمای کلی از یک هموارسازی مرتبه بالاتر داشته باشید، “تاخیر کل” برابر با میانگین تاخیرها است. به عنوان مثال، اگر از یک سفارش سوم هموارسازی با تاخیر کلی 3 ماهه استفاده کنید (به این معنی که تاخیرهای هر مرحله هر کدام برابر با یک ماه است) برای نشان دادن اینکه چگونه خریداران به تدریج درک خود از قیمت را تنظیم میکنند، متوسط خریداران برداشت خود را به طور کامل در 3 ماه تنظیم میکند. – البته برخی از خریداران سریع تر و برخی دیگر با سرعت کمتری نسبت به میانگین خود را تطبیق میدهند.


 نمونههای کلاسیک:
نمونههای کلاسیک: