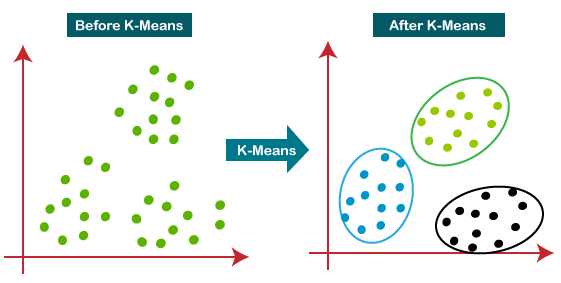
الگوریتمی برای گروه بندی n مشاهده در k خوشه است که از کوانتیزاسیون برداری استفاده میکند. این الگوریتم یک روش برای خوشه بندی دادهها در یادگیری بدون نظارت است. این الگوریتم به طور مکرر نقاط داده را با به حداقل رساندن واریانس در هر خوشه به k خوشه تقسیم میکند
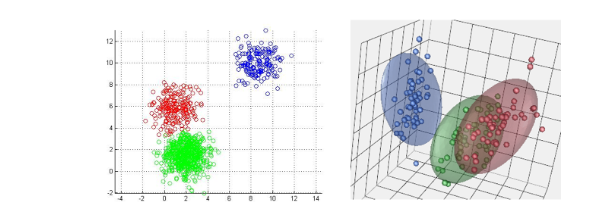
خوشه بندی k-means یک الگوریتم خوشه بندی انحصاری است. هر شی دقیقاً به یکی از خوشهها اختصاص داده شده است. (روشهای دیگری وجود دارد که به اشیا اجازه میدهد در بیش از یک خوشه قرار بگیرند). برای این روش خوشهبندی، ما با تصمیمگیری در مورد تعداد خوشه شروع میکنیم که میخواهم دادههای ما را شامل شود. ما این مقدار را k مینامیم. مقدار k به طور کلی یک عدد صحیح کوچک، مانند 2، 3، 4 یا 5 است، اما ممکن است بزرگتر باشد. بعدا به این سؤال که تعداد مناسب K چقدر باید باشد صحبت میکنیم.
راههای زیادی وجود دارد که در آنها k خوشه به طور بالقوه ممکن است، تشکیل شوند. ما میتوانیم کیفیت مجموعه ای از خوشهها را با استفاده از مقدار یک هدف اندازه گیری کنیم. این تابع هدف میتواند مجموع مجذور فواصل باشد. فاصله عبارت است از فاصله هر نقطه از مرکز خوشه ای که به آن اختصاص داده شده است. ما میخواهیم مقدار این تابع تا حد امکان کوچک باشد. حال k نقطه اول را به صورت تصادفی انتخاب میکنیم. اینها به عنوان مرکز K خوشه، در نظر گرفته می شوند. مرکزهای k خوشه بالقوه در ابتدا هیچ عضوی ندارند. ما میتوانیم این نقاط را به هر شکلی که میخواهیم انتخاب کنیم، اما شاید بهتر باشد k نقطه اولیه را به گونه ای انتخاب کنیم که نسبتاً از هم فاصله داشته باشند. اکنون هر یک از نقاط را یکی یکی به خوشه ای که دارای کمترین فاصله است اختصاص می دهیم یعنی نزدیکترین مرکز هنگامی که تمام اشیاء اختصاص داده شدند، k خوشه بر اساس آن خواهیم داشت k مرکز اصلی اما «مرکزیت ها» دیگر مرکز واقعی آن نخواهند بود. سپس مرکزهای خوشهها را مجدداً محاسبه میکنیم و سپس آن را تکرار میکنیم
📌 کاربرد الگوریتم K-Means
- بازاریابی: میتوان از آن برای شناسایی و کشف بخش های مشتری برای اهداف بازاریابی استفاده کرد.
- زیست شناسی: میتوان از آن برای طبقهبندی در میان گونههای مختلف گیاهی و جانوری استفاده کرد.
- کتابخانهها: در خوشهبندی کتابهای مختلف بر اساس موضوعات و اطلاعات استفاده میشود.
- بیمه: برای شناسایی مشتریان، سیاستهای آنها و شناسایی تقلب ها استفاده میشود.
- برنامهریزی شهری: برای گروهبندی خانهها و بررسی ارزش آنها بر اساس موقعیت جغرافیایی و سایر عوامل موجود استفاده میشود.
- مطالعات زلزله : با یادگیری مناطق زلزله زده میتوان مناطق خطرناک را تعیین کرد.
📌 معایب الگوریتم K-Means
- فقط زمانی قابل اجراست که میانگین تعریف شده باشد
- باید k، تعداد خوشه ها را از قبل مشخص کنید
- با داده های مغشوش و پرت مشکل دارد
- برای کشف خوشههایی با اشکال غیر محدب مناسب نیست
- هنگامی که خوشه ها متفاوت هستند K-means محدودیتهایی دارد :
- اندازه ها
- تراکم ها
- اشکال غیر کروی
محدودیتهای K-means: اندازههای مختلف
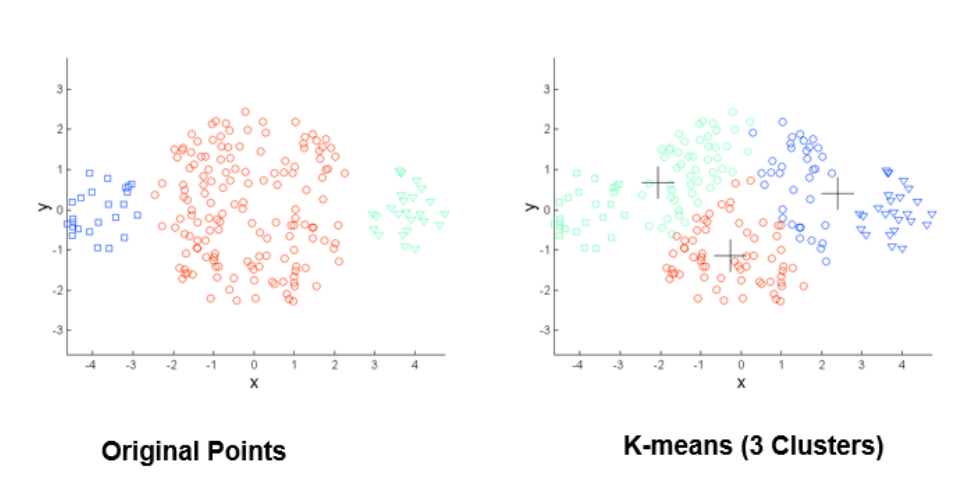
محدودیتهای K-means: اشکال غیر کروی
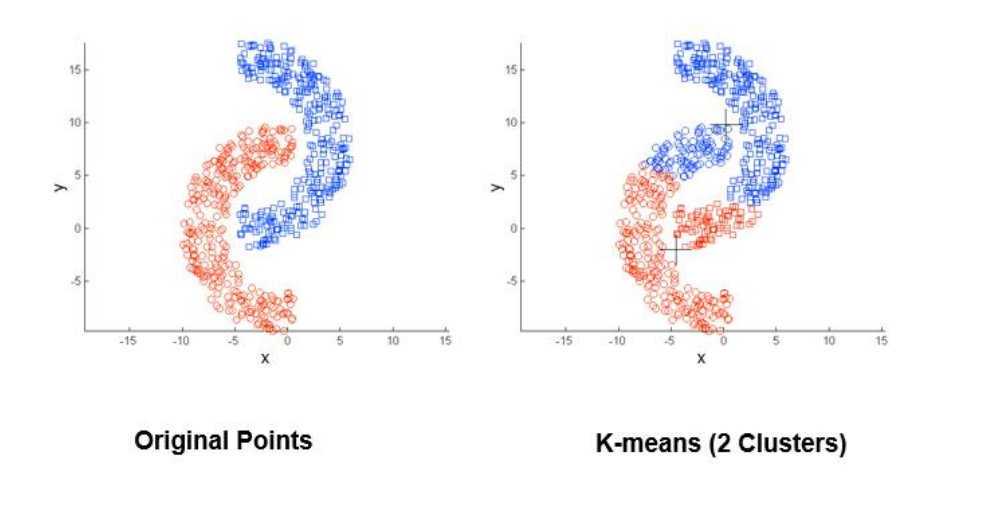
محدودیتهای K-means: تراکم متفاوت
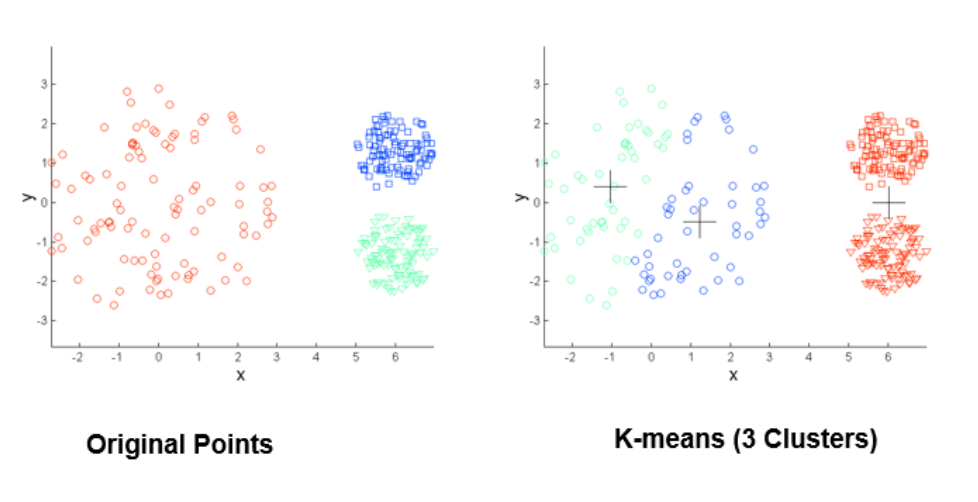
📌 روش کار الگوریتم K-Means
این روش مبنتی بر مرکز است. برای محاسبه فاصله، از فاصله اقلیدوسی استفاده میکنیم .
- ابتدا باید ماتریس فاصله را محاسبه کنیم | برای محاسبه فاصله نقاط از هم و ساخت ماتریس فاصله از فرمول فاصله اقلیدوسی استفاده میکنیم Dis ((x,y),(a,b)) = √(x-a)2 + (y-b)2
- از بین نقاط k نقطه را انتخاب میکنیم و هر نقطه را یک خوشه در نظر میگیریم | روش elbow به ما امکان میدهد اینرسی را رسم کنیم و نقطهای که داده در آن شروع به کاهش خطی میکند را پیدا کنیم. نقطه کاهش همان مقدار K ما است که به آن نقطه ضربه نیز میگویند
- در این مرحله فاصله هر نقطه را با تک تک خوشهها محاسبه میکنیم با استفاده از فاصله اقلیدوسی و نقطه ای که فاصله کمتری با مرکز خوشهها دارد وارد آن خوشه میشود. این کار را برای تمام نقاط انجام میدهیم
- پس از اتمام مرحله سوم مجدد باید یک مرکز جدید برای خوشهها محاسبه کنیم. برای اینکار باید میانگین نقاط داخل هر خوشه را محاسبه کنیم. این میانگین نشان دهنده مختصات مرکز جدید خوشه است ((x1+x2+…+xn / n),(y1+y2+…+yn / n))
- در این مرحله با استفاده از فاصله ی اقلیدوسی فاصله نقاط تا مرکز هر K خوشه را محاسبه میکنیم و نقاط به هر مرکزی نزدیکتر بودند وارد خوشه ی آن مرکز میشوند
- این فرآیند تا زمانی انتقال پیدا میکند که دیگر هیچ جابجایی نقطهای نداشته باشیم در این صورت خوشهها به بهینگی رسیدند



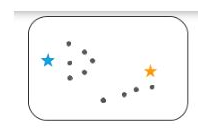
فرض کنید دو متغیر M1 و M2 داریم. نمودار پراکندگی محور x-y این دو متغیر در زیر آورده شده است:

برای شناسایی مجموعه داده ها و قرار دادن آنها در خوشه های مختلف، عدد k از خوشه ها را در نظر می گیریم، یعنی K=2. یعنی در اینجا سعی خواهیم کرد این مجموعه داده ها را در دو خوشه مختلف گروه بندی کنیم.
برای تشکیل خوشه باید k نقطه یا مرکز تصادفی را انتخاب کنیم. این نقاط می توانند نقاطی از مجموعه داده یا هر نقطه دیگری باشند. بنابراین، در اینجا ما دو نقطه زیر را به عنوان K نقطه انتخاب میکنیم که بخشی از مجموعه داده ما نیستند. تصویر روبرو را در نظر بگیرید:
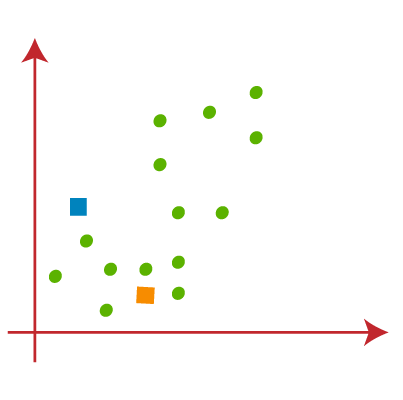
اکنون هر نقطه داده نمودار پراکندگی را به نزدیکترین نقطه K یا مرکز آن اختصاص میدهیم. ما آن را با استفاده از ریاضیاتی که برای محاسبه فاصله بین دو نقطه مطالعه کردهایم محاسبه خواهیم کرد. بنابراین، ما یک میانه بین هر دو مرکز ترسیم میکنیم. تصویر روبرو را در نظر بگیرید:
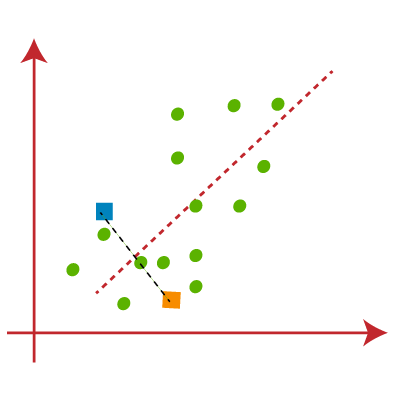
از تصویر بالا مشخص است که نقاط سمت چپ خط نزدیک به مرکز K1 یا آبی است و نقاط سمت راست خط نزدیک به مرکز زرد است. برای تجسم واضح، آنها را به رنگ آبی و زرد رنگ تبدیل میکنیم.
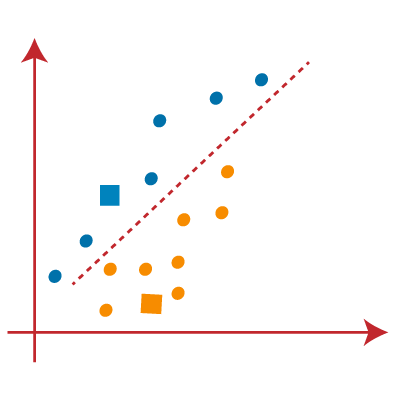
حال باید نزدیکترین خوشه را پیدا کنیم، با انتخاب یک مرکز جدید، این فرآیند را تکرار خواهیم کرد. برای انتخاب مرکزهای جدید، مرکز ثقل یا میانگین دادههای هر خوشه را محاسبه کرده و مرکزهای جدید را به صورت روبرو پیدا خواهیم کرد:
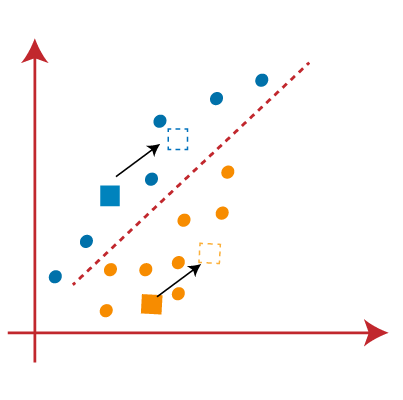
در مرحله بعد، هر نقطه داده را به مرکز جدید اختصاص می دهیم. برای این کار، همان فرآیند یافتن خط میانه را تکرار میکنیم. میانگین مانند تصویر زیر خواهد بود:
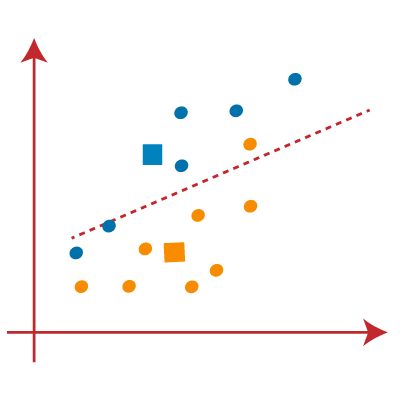
از تصویر بالا میبینیم که یک نقطه زرد در سمت چپ خط و دو نقطه آبی رنگ درست به خط قرار دارند. بنابراین، این سه نقطه به مرکزهای جدید اختصاص داده میشود.
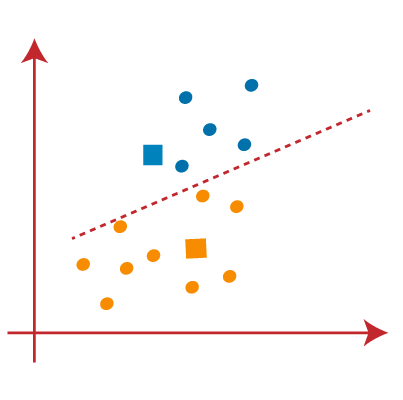
همانطور که تخصیص مجدد انجام میشود، ما دوباره به مرحله 4 خواهیم رفت، که یافتن مرکزها یا نقاط K جدید است.
ما این فرآیند را با یافتن مرکز ثقل تکرار می کنیم، بنابراین مرکزهای جدید مانند تصویر روبرو خواهند بود:
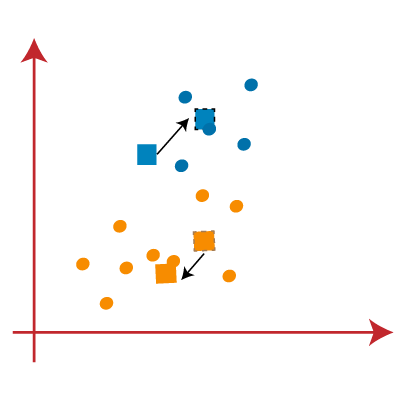
همانطور که ما مرکز جدید را یافتهایم، دوباره خط میانه را رسم می کنیم و نقاط داده را دوباره اختصاص می دهیم. بنابراین، تصویر به صورت زیر خواهد بود:
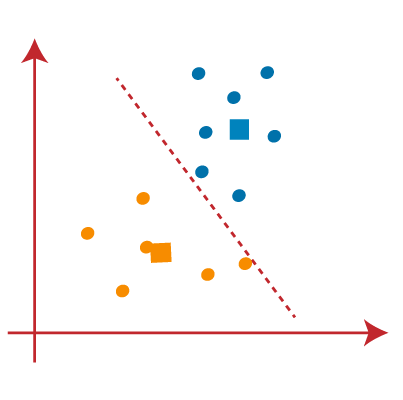
در تصویر بالا می بینیم؛ هیچ نقطه داده متفاوتی در دو طرف خط وجود ندارد، به این معنی که مدل ما شکل یافته است. تصویر روبرو را در نظر بگیرید:
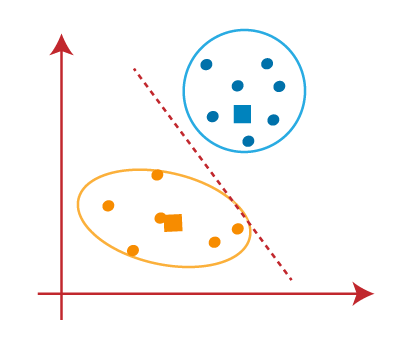
همانطور که مدل ما آماده است، اکنون می توانیم مرکزهای فرضی را حذف کنیم و دو خوشه نهایی مانند تصویر روبرو خواهند بود:
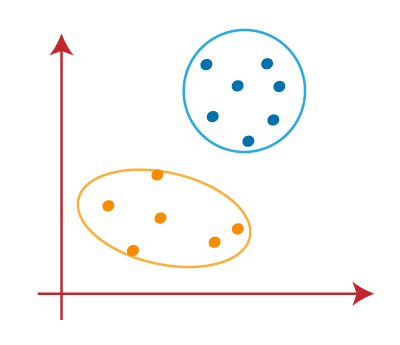
 محاسبه کیفیت خوشهها
محاسبه کیفیت خوشهها
مجموع توان دوم فواصل نقاط تا مرکز خوشه
E = Σk I=1 Σ dist(p.ci)2
محاسبه ی k
عملکرد الگوریتم خوشه بندی K-means به خوشههای بسیار کارآمدی که تشکیل میدهد بستگی دارد. اما انتخاب تعداد بهینه خوشهها کار بزرگی است. روشهای مختلفی برای یافتن تعداد بهینه خوشهها وجود دارد، اما در اینجا ما مناسبترین روش برای یافتن تعداد خوشهها یا مقدار K را مورد بحث قرار میدهیم. این روش در زیر آورده شده است:
Elbow Method
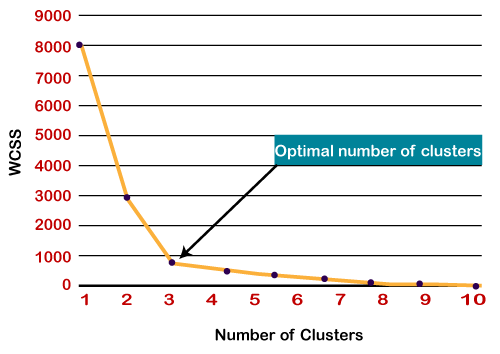
روش زانو یکی از محبوبترین روشها برای یافتن تعداد بهینه خوشهها است. این روش از مفهوم مقدار WCSS استفاده میکند. WCSS مخفف عبارت Within Cluster Sum of Squares است که کل تغییرات را در یک خوشه تعریف میکند. فرمول محاسبه مقدار WCSS (برای 3 خوشه) در زیر آمده است:
WCSS= ∑Pi in Cluster1 distance(Pi C1)2 +∑Pi in Cluster2distance(Pi C2)2+∑Pi in CLuster3 distance(Pi C3)2
برای یافتن مقدار بهینه خوشه ها، روش زانویی مراحل زیر را دنبال می کند:
- خوشه بندی K-means را بر روی یک مجموعه داده معین برای مقادیر مختلف K (محدوده 1-10) اجرا می کند.
- برای هر مقدار K، مقدار WCSS را محاسبه می کند.
- منحنی بین مقادیر محاسبهشده WCSS و تعداد خوشههای K ترسیم میکند.
- نقطه تیز خم یا یک نقطه از طرح شبیه یک بازو است، سپس آن نقطه به عنوان بهترین مقدار K در نظر گرفته می شود.
از آنجایی که نمودار خم تیز را نشان میدهد که شبیه یک آرنج است، از این رو به روش آرنج معروف است. نمودار روش آرنج مانند تصویر زیر است:
مثالهای کاربردی
📌 مثال عددی-1
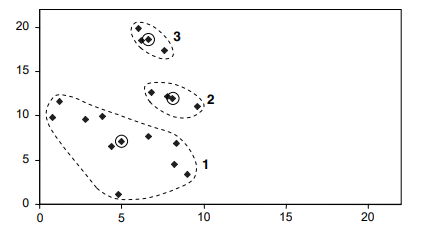
ما الگوریتم k-means را برای خوشه بندی 16 شیء نشان خواهیم داد. با دو ویژگی x و y که در شکل زیر فهرست شدهاند. 16 نقطه مربوط به این اشیا به صورت نموداری نشان داده شده است. محورهای افقی و عمودی با ویژگیهای x و مطابقت دارند y به ترتیب.
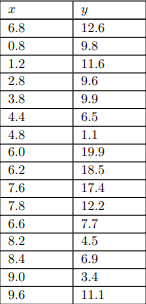
سه تا از نقاط نشان داده شده در شکل بالا با دایرههای کوچکی احاطه شدهاند. فرض می کنیم k = 3 و این سه نقطه را انتخاب کردهایم به عنوان مکان سه مرکز اولیه انتخاب شدهاند. این اولیه انتخاب (نسبتا دلخواه) در شکل زیر نشان داده شده است

نقاط d1، d2 و d3 در شکل زیر فاصله اقلیدسی هر یک از 16 نقطه را از سه مرکز نشان می دهند. برای اهداف در این مثال، ما هیچ یک از ویژگی ها را نرمال یا موزون نمیکنیم، بنابراین فاصله اولین نقطه (6.8، 12.6) از مرکز اول (3.8، 9.9) به سادگی است.
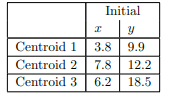
ستونی با عنوان «خوشه» نزدیکترین مرکز به هر نقطه را نشان میدهد بنابراین خوشه ای که باید به آن اختصاص داده شود
خوشه های به دست آمده در شکل بالا در زیر نشان داده شده است.
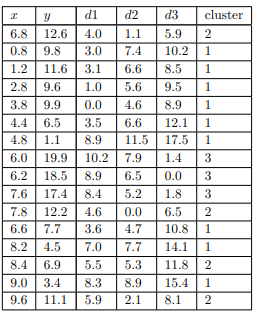
مرکزها با دایره های کوچک نشان داده میشوند. برای این اولین تکرار آنها هستند. همچنین نقاط واقعی درون خوشهها. مرکزها آنهایی هستند که مورد استفاده قرار گرفتند. برای ساختن سه خوشه اما مرکز واقعی خوشهها پس از ایجاد آنها نیستند. سپس مرکزهای سه خوشه را با استفاده از مقادیر x و y محاسبه میکنیم. از اشیایی که در حال حاضر به هر یک اختصاص داده شده است. نتایج در شکل نشان داده شده است
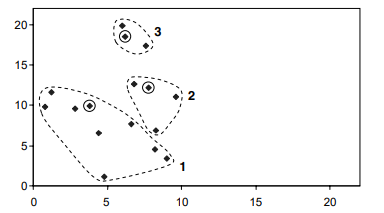
سه مرکز همگی با فرآیند تخصیص جابهجا شدهاند، اما حرکت مرکز سوم بهطور قابلتوجهی کمتر از دو مرکز دیگر است. سپس با تعیین اینکه فاصله هریک از نقاط از مراکز جدید، 16 شی را به سه خوشه اختصاص میدهیم .
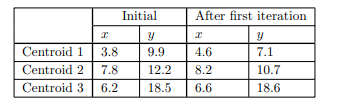
مرکزها دوباره با دایرههای کوچک نشان داده میشوند. با این حال از این به بعد مرکزها “نقاط خیالی” مربوط به “مرکز” هر خوشه هستند، نقاط واقعی درون خوشهها نیست. در واقع فقط یک نقطه جابجا شده است. شیء موجود در (8.3، 6.9) از خوشه 2 به خوشه 1 منتقل شده است. سپس موقعیت سه مرکز را دوباره محاسبه میکنیم.
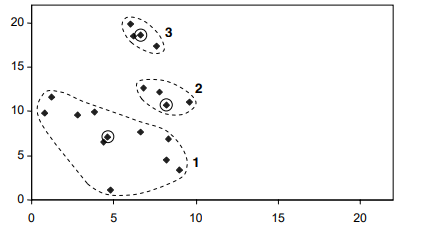
دو مرکز اول کمی حرکت کردهاند، اما سومی اصلا حرکت نکرده است. ما 16 شیء را یک بار دیگر به خوشه ها اختصاص میدهیم
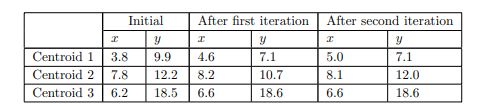
اینها همان خوشههای قبلی هستند. مرکز آنها مانند آنهایی است که خوشهها از آنها ایجاد شده اند. از این رو شرط خاتمه الگوریتم k-means “تکرار … تا زمانی که مرکزها دیگر حرکت نکنند” برآورده شده است و اینها خوشههای نهایی هستند که توسط الگوریتم برای انتخاب اولیه مرکز ساخته شده تولید می شوند.
📌 مثال عددی-2
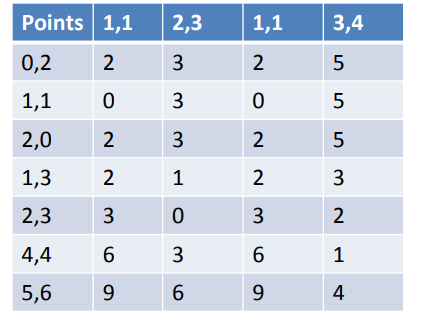
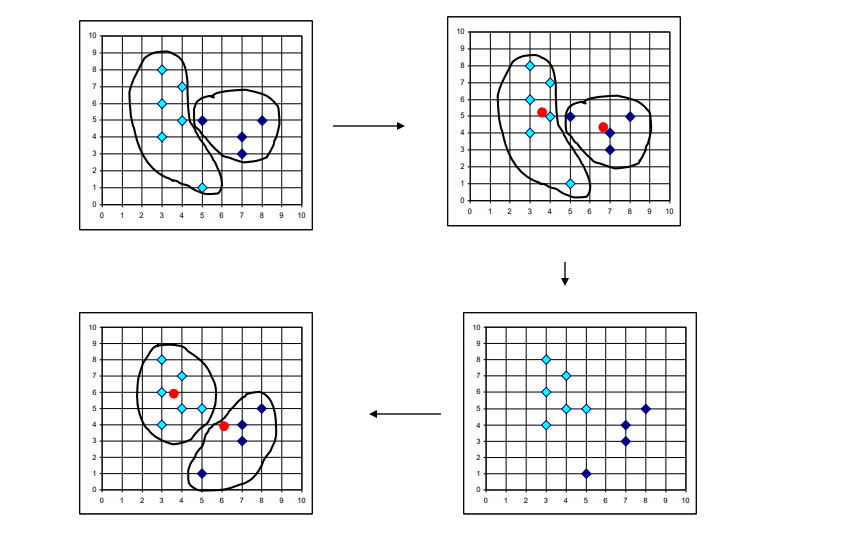
- دو تکرار از الگوریتم خوشه بندی k-means را برای نقاط داده زیر نشان دهید.
- فرض کنید k=2 و میانگین خوشه اولیه (1,1) باشد. (2،3).
- پس از هر تکرار، معنی و محتویات خوشه ها را ارائه دهید.
- از متریک فاصله منهتن استفاده کنید.
C1: 0,2 1,1 2,0 M1: 1,1
C2: 1,3 2,3 4,4 5,6 M2:3,4
C1: 0,2 1,1 2,0 1,3 M1: 1,6/4
C2: 2,3 4,4 5,6 M2:11/3,13/3
💻کدنویسی
📌 کد پایتونی
import pandas as pd
import numpy as np
import random as rd
import matplotlib.pyplot as plt
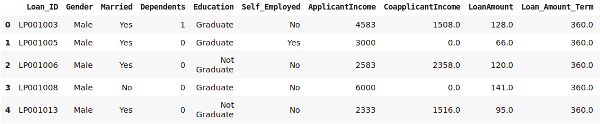
data = pd.read_csv('clustering.csv')
data.head()
#number of clusters
K=3
# Select random observation as centroids
Centroids = (X.sample(n=K))
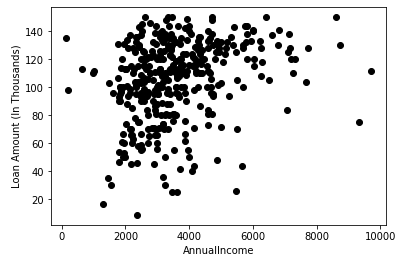
plt.scatter(X["ApplicantIncome"],X["LoanAmount"],c='black')
plt.scatter(Centroids["ApplicantIncome"],Centroids["LoanAmount"],c='red')
plt.xlabel('AnnualIncome')
plt.ylabel('Loan Amount (In Thousands)')
plt.show()
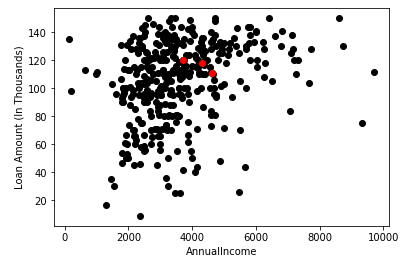
در اینجا، نقاط قرمز نشان دهنده 3 مرکز برای هر خوشه است. توجه داشته باشید که ما این نقاط را به طور تصادفی انتخاب کرده ایم و از این رو هر بار که این کد را اجرا می کنید، ممکن است سانترویدهای مختلفی دریافت کنید.
# Step 3 - Assign all the points to the closest cluster centroid
# Step 4 - Recompute centroids of newly formed clusters
# Step 5 - Repeat step 3 and 4
diff = 1
j=0
while(diff!=0):
XD=X
i=1
for index1,row_c in Centroids.iterrows():
ED=[]
for index2,row_d in XD.iterrows():
d1=(row_c["ApplicantIncome"]-row_d["ApplicantIncome"])**2
d2=(row_c["LoanAmount"]-row_d["LoanAmount"])**2
d=np.sqrt(d1+d2)
ED.append(d)
X[i]=ED
i=i+1
C=[]
for index,row in X.iterrows():
min_dist=row[1]
pos=1
for i in range(K):
if row[i+1] < min_dist:
min_dist = row[i+1]
pos=i+1
C.append(pos)
X["Cluster"]=C
Centroids_new = X.groupby(["Cluster"]).mean()[["LoanAmount","ApplicantIncome"]]
if j == 0:
diff=1
j=j+1
else:
diff = (Centroids_new['LoanAmount'] - Centroids['LoanAmount']).sum() + (Centroids_new['ApplicantIncome'] - Centroids['ApplicantIncome']).sum()
print(diff.sum())
Centroids = X.groupby(["Cluster"]).mean()[["LoanAmount","ApplicantIncome"]]
color=['blue','green','cyan']
for k in range(K):
data=X[X["Cluster"]==k+1]
plt.scatter(data["ApplicantIncome"],data["LoanAmount"],c=color[k])
plt.scatter(Centroids["ApplicantIncome"],Centroids["LoanAmount"],c='red')
plt.xlabel('Income')
plt.ylabel('Loan Amount (In Thousands)')
plt.show()
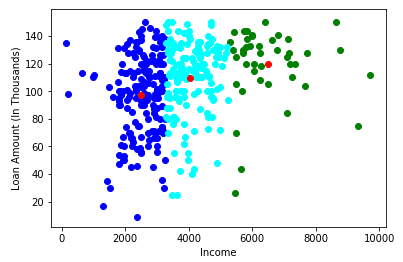


 محاسبه کیفیت خوشهها
محاسبه کیفیت خوشهها 

