مقدمه
دادههای پرت (Outliers) در نگاه اول فقط چند نقطهی عجیب و دورافتاده به نظر میرسند، اما در واقع یکی از تعیینکنندهترین عوامل در کیفیت تحلیل، اعتبار مدلها و حتی تصمیمگیریهای سازمانی هستند. مجموعهای که اکنون پیش روی شماست، یک راهنمای مرحلهبهمرحله، جامع و کاربردی دربارهی شناخت، منشأ، انواع، اثرات و روشهای مدیریت دادههای پرت در تحلیل داده، آمار و یادگیری ماشین است.
در چهار بخش نخست این مجموعه، بهصورت لایهبهلایه پیش رفتیم:
۱. در بخش اول
ماهیت دادههای پرت را تعریف کردیم، تفاوت آنها با «نویز» را توضیح دادیم و نشان دادیم چرا Outlierها همیشه بد نیستند و گاهی حتی نقش سیگنالهای حیاتی را دارند.
۲. در بخش دوم
به دلایل بروز دادههای پرت، طبقهبندی آنها (پرتهای نقطهای، زمینهمحور، سیستمی، چندبعدی) و چرایی خطرناکبودنشان در تحلیلهای آماری پرداختیم.
۳. در بخش سوم
وارد دنیای عملی مدیریت دادههای پرت شدیم:روشهای حذف، اصلاح، Winsorizing، مدلسازی صریح Outlier، انتخاب بین نگهداری یا حذف و اثر این تصمیمها بر تفسیر نتایج.
۴. در بخش چهارم
نشان دادیم که دادههای پرت چه اثرات عظیمی بر تحلیلهای آماری و یادگیری ماشین دارند:تحریف میانگین و واریانس، نقض مفروضات مدلها، گمراهکردن رگرسیون، منحرفکردن PCA، ایجاد رابطههای ساختگی، آلودهکردن آزمونهای آماری و حتی آسیب به شبکههای عصبی.
اکنون در بخش پنجم وارد حوزهای پیچیدهتر و تخصصیتر میشویم:
۵. دادههای پرت در سریهای زمانی
سریهای زمانی ساختاری پویا و وابسته به زمان دارند، بنابراین Outlierها در آنها تنها یک نقطهی اشتباه نیستند؛ممکن است اثرشان به چندین مشاهده بعدی سرایت کند، یا بیانگر شکست ساختاری، رویداد ناگهانی یا تغییر رژیم تولید داده باشند.
در این بخش بهطور کامل بررسی شد:
- انواع Outlierهای سری زمانی (AO، IO، LS، TC)
- دلایل بروز ناهنجاری در دادههای وابسته به زمان
- اثرات Outlier بر تخمین پارامتر، ACF/PACF، پیشبینی و آزمونها
- روشهای تشخیص آماری، مدلمحور و یادگیری ماشین
- مدیریت Outlier با حذف، جایگزینی، مدلسازی صریح و روشهای مقاوم
- چالشهایی مانند Masking، Swamping، ناایستایی و چندبعدیبودن
5.1 تعریف و انواع دادههای پرت در سریهای زمانی
در دادههای مقطعی، معمولاً فرض استقلال بین مشاهدات قابل قبول است؛ اما در سریهای زمانی، وابستگی زمانی ویژگی اصلی داده است. همین وابستگی باعث میشود یک دادهی پرت نهفقط همان نقطه، بلکه رفتار مشاهدات بعدی را هم تحت تأثیر قرار دهد. به همین دلیل، تعریف و شناسایی دادهی پرت در سریهای زمانی پیچیدهتر از دادههای مقطعی است.
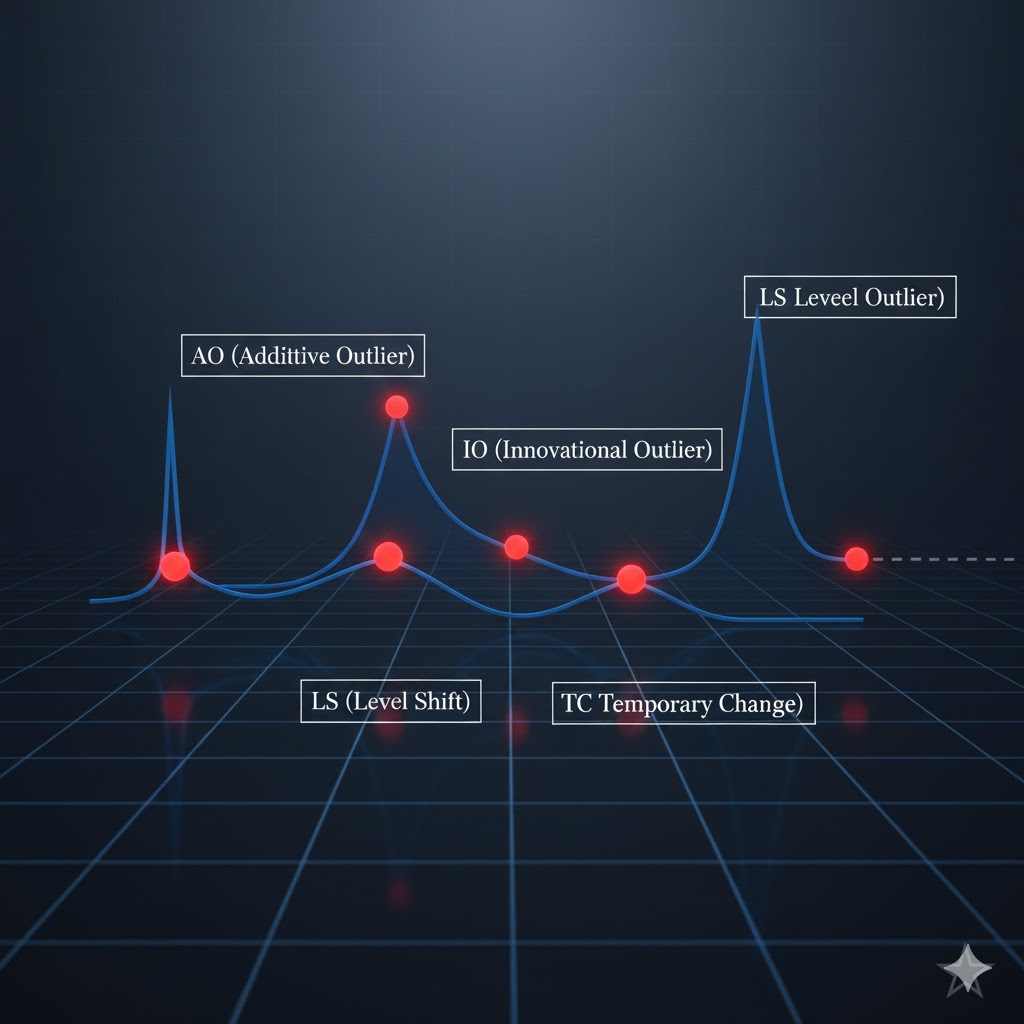
انواع رایج دادههای پرت در سریهای زمانی عبارتاند از:
دادهی پرت افزایشی (Additive Outlier – AO)
- یک جهش غیرعادی در یک مشاهدهی منفرد که بهطور موقّت الگوی سری را بههم میزند.
- پس از این نقطه، سری معمولاً به رفتار قبلی خود بازمیگردد.
- شبیه یک خطای اندازهگیری بزرگ یا یک رویداد ناگهانی و گذرا است.
دادهی پرت نوآورانه (Innovational Outlier – IO)
- به جای خودِ مقدار مشاهده، بر نوآوری یا جملهی خطا در یک زمان خاص اثر میگذارد.
- به دلیل ساختار پویای سری (مثلاً در مدل ARIMA)، اثر آن به مشاهدات بعدی سرایت میکند و میتواند اثر ماندگار داشته باشد.
تغییر سطح (Level Shift – LS)
- بیانگر تغییر ناگهانی و تقریباً دائمی در سطح میانگین سری از یک زمان خاص به بعد است.
- اغلب ناشی از مداخلهی بیرونی (مثلاً تغییر سیاست، راهاندازی خط تولید جدید، تغییر رژیم بازار) یا شکست ساختاری در فرآیند است.
تغییر موقت (Temporary Change – TC)
- شبیه IO است با این تفاوت که اثر آن بر مشاهدات بعدی به تدریج و معمولاً نمایی کاهش مییابد و در نهایت از بین میرود.
- رویدادی را منعکس میکند که شوک اولیهی قوی دارد، اما سیستم بهتدریج به سطح عادی برمیگردد.
تمایز بین AO، IO، LS و TC در عمل بسیار مهم است، زیرا هرکدام روشهای تشخیص و مدلسازی خاص خود را میطلبند .
| بهترین روش تشخیص | مثال واقعی | اثر بر سری زمانی | تعریف دقیق | نوع Outlier |
|---|---|---|---|---|
| Z-score روی پسماند، Boxplot | خرابی لحظهای سنسور | اثر کوتاهمدت؛ سری بلافاصله به مسیر قبلی برمیگردد | یک پرش ناگهانی و تکنقطهای در مقدار سری | AO – Additive Outlier |
| برازش اولیه ARIMA + تحلیل پسماند | شوک ناگهانی اقتصادی | اثر در چند مشاهده بعدی پخش میشود و ماندگارتر است | پرت در جمله خطا (innovation) مدل ARIMA | IO – Innovational Outlier |
| آزمون ساختار شکستی، تحلیل پسماند | تغییر سیاست دولت، تغییر نرخ ارز | تغییر سطح میانگین برای همیشه | تغییر ناگهانی و دائمی در سطح سری | LS – Level Shift |
| ARIMA + بررسی decay پسماند | قطعی موقت سیستم، حمله سایبری کوچک | اثر نمایی کاهنده | تغییر ناگهانی که اثرش به تدریج محو میشود | TC – Temporary Change |
5.2 علل بروز دادههای پرت در سریهای زمانی
دادههای پرت میتوانند از مجموعهای متنوع از منابع ناشی شوند، از جمله:
- خطاهای اندازهگیری یا ورود داده:خطای انسانی در ثبت، خرابی یا کالیبراسیون نامناسب سنسور، نقص تجهیزات ثبت داده.
- رویدادهای نادر و غیرمنتظره:بلایای طبیعی (سیل، زلزله)، بحرانهای اقتصادی، اعتصابات، همهگیریها، حوادث صنعتی، تغییر ناگهانی نرخ ارز و… .
- تغییرات ساختاری در فرآیند:تغییر در تکنولوژی تولید، تغییر الگوی مصرف، اجرای سیاست جدید، تغییر در قوانین و مقررات.
- خطاهای نمونهگیری:انتخاب نمونههایی که نمایندهی واقعی فرآیند نیستند یا بهطور تصادفی مقادیری بسیار غیرمعمول را شامل میشوند.
- رفتار ذاتی فرآیند:برخی فرآیندها ذاتاً «جهشی» و با دمهای سنگیناند (مثلاً بازارهای مالی)، بنابراین دادههای ظاهراً پرت، بخشی از ماهیت طبیعی فرآیند محسوب میشوند.
5.3تأثیر دادههای پرت بر تحلیل سریهای زمانی
وجود دادههای پرت در سریهای زمانی میتواند پیامدهای متعددی داشته باشد:
تخمین پارامتر
تخمینگرهای کلاسیک (مثل حداقل مربعات) نسبت به نقاط دورافتاده بسیار حساساند؛ حضور چند دادهی پرت میتواند پارامترهای ARIMA یا مدلهای مشابه را به شدت منحرف کند و منجر به برآوردهای مغرضانه و ناکارا شود .
شناسایی مدل (Model Identification)
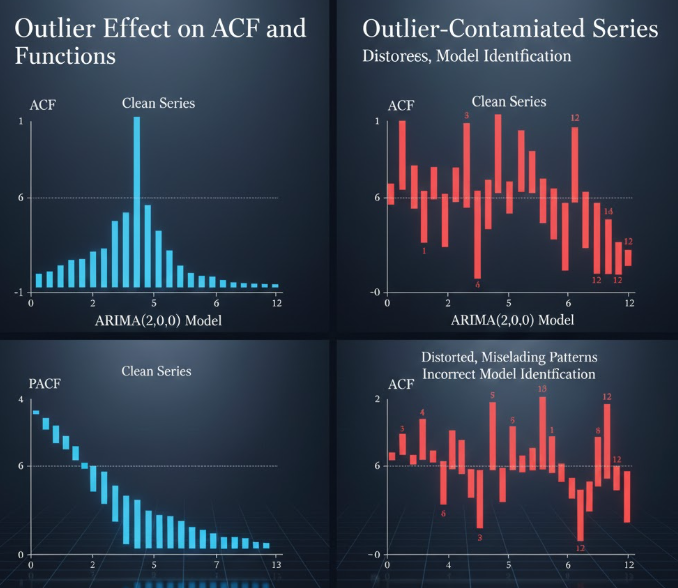
دادههای پرت میتوانند ACF و PACF نمونهای را تحریف کنند و انتخاب مرتبهی مناسب مدل (p, d, q) را گمراه سازند؛ در نتیجه ممکن است مدل اشتباه انتخاب شود.
پیشبینی
مدلی که برای توضیح نقاط غیرعادی «خود را کجومعوج» کرده است، معمولاً روی دادههای آینده عملکرد خوبی ندارد؛ پیشبینیها ناپایدار و غیرقابل اعتماد میشوند.
آزمونهای آماری
آزمونهای مانایی، آزمونهای اهمیت پارامترها و سایر آزمونهای فرض به حضور دادههای پرت حساساند و ممکن است قدرت یا سطح خطای آنها بهطور جدی مخدوش شود.
تحلیل روابط در سریهای زمانی چندمتغیره
چند نقطهی پرت میتوانند همبستگیهای ساختگی بین سریها ایجاد کنند یا روابط واقعی را پنهان کنند؛ بهخصوص زمانی که فقط یکی از سریها تحت تأثیر شوک شدید قرار گرفته است.
5.4اثرات دادههای پرت بر مدلهای مختلف سری زمانی
دادههای پرت، بسته به نوع مدل سریزمانی، اثرات متفاوت و گاهی بسیار عمیقی دارند.در این بخش اثرات Outlier بر مدلهای پرکاربرد را دقیقتر بررسی میکنیم:
الف) اثر Outlier بر مدلهای AR، MA و ARIMA
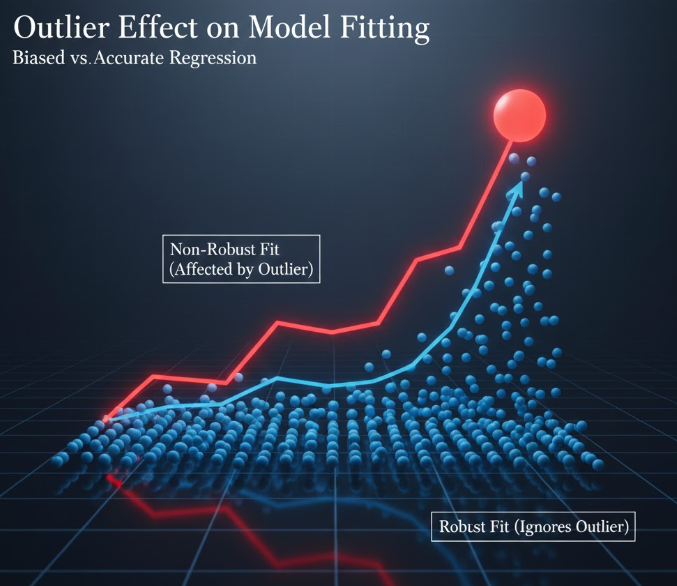
مشکلات اصلی:
- تحریف شدید در برآورد پارامترها
حتی یک AO میتواند AR(1) یا ARIMA را وادار به تخمین ضرایب اشتباه کند. - خراب کردن ACF و PACF
باعث میشود p و q اشتباه انتخاب شوند. - پیشبینی ناپایدار
چون مدل خودش را برای توضیح یک نقطه پرت «کج» میکند.
چرا این اتفاق میافتد؟
ARIMA اساساً بر پایه حداقل مربعات است و Outlierها واریانس را منفجر میکنند.
ب) اثر Outlier بر مدلهای Exponential Smoothing (ETS)
در ETS مانند: Holt-Winters
- Outlier سطح (Level) را منحرف میکند
- یا روند (Trend) را دچار پرش میکند
- هموارسازی ممکن است چندین گام زمان ببرد تا به مسیر واقعی برگردد
ج) اثر Outlier بر Prophet (مدل فیسبوک)
Prophet نسبت به Level Shift مقاومتر استاما نسبت به AO و IO حساس است.
مشکلات:
- پرش یکنقطهای در داده باعث spike ناگهانی در پیشبینی میشود
- نیاز به استفاده از holidays یا extra regressors دارد
د) اثر Outlier بر مدلهای یادگیری عمیق (LSTM / GRU / CNN)
Outlier باعث:
- Gradient Explosion
- ورود به نواحی اشباع
- رفتار غیرقابلپیشبینی
- کاهش پایداری آموزش
راهکار:
- Robust Scaling
- حذف یا Winsorize
- Lossهای مقاوم (Huber Loss)
هـ) اثر Outlier در مدلهای چندمتغیره (VAR، VECM)
- Outlier در یکی از سریها میتواند روابط کل سیستم را تخریب کند
- باعث ایجاد همبستگی ساختگی یا پنهان کردن رابطه واقعی میشود
- بر آزمونهای علیت گرنجر اثر مستقیم میگذارد
5.5 روشهای تشخیص دادههای پرت در سریهای زمانی
بهطور کلی، روشهای تشخیص دادهی پرت در سریهای زمانی را میتوان به سه دستهی اصلی تقسیم کرد: آماری، مبتنی بر مدل و مبتنی بر یادگیری ماشین/دادهکاوی.
5.5.1روشهای آماری ساده
نمرهی Z و نمرهی Z مقاوم
استفاده از Z-score کلاسیک یا نسخهی اصلاحشدهی آن بر اساس MAD. این روشها معمولاً فرض میکنند دادهها (یا پسماندهای مدل) نرمالاند. در سریهای زمانی، بهتر است بهجای خود سری، روی پسماندهای مدل اعمال شوند.
نمودار جعبهای (Boxplot)
شناسایی نقاط خارج از بازهی . Q1 – 1.5 IQR, Q3+1.5IQR این روش هم در اصل تکمتغیره و بدون توجه به وابستگی زمانی است.
آزمونهای Grubbs و Dixon
برای شناسایی یک یا دو نقطهی دورافتاده طراحی شدهاند؛ اما مثل روشهای قبل، استقلال مشاهدات را فرض میکنند و در سریهای زمانی باید با احتیاط و اغلب بر روی پسماندها استفاده شوند.
5.5.2روشهای مبتنی بر مدل
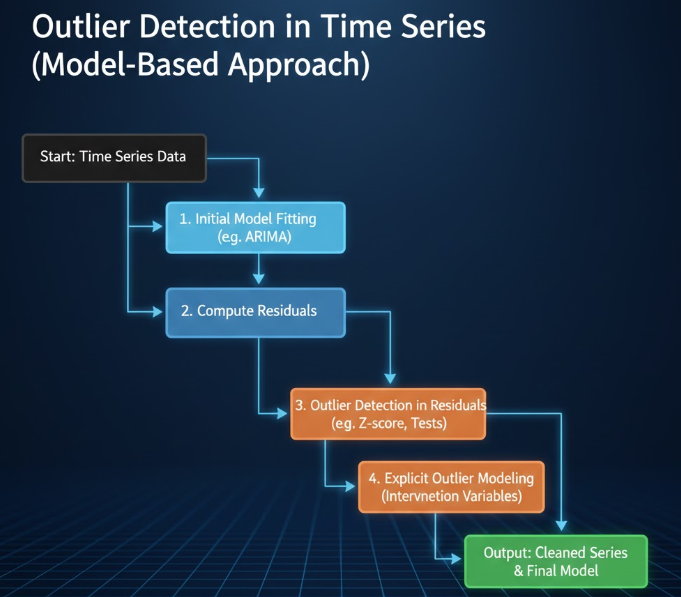
تحلیل پسماند
یک مدل سری زمانی )مثل ARIMA) روی دادهها برازش میدهیم، سپس پسماندها را بررسی میکنیم؛ پسماندهایی که از حد مشخصی فراتر میروند میتوانند نشاندهندهی دادهی پرت باشند.
تحلیل مداخله و مدلسازی صریح دادهی پرت
رویکرد Box & Tiao و توسعهی آن توسط Chen & Liu این است که انواع مختلف دادهی پرت (AO، IO، LS، TC) را بهشکل متغیرهای مداخله در مدل ARIMA وارد کنیم و همزمان نوع، زمان وقوع و بزرگی آنها را تخمین بزنیم. الگوریتمهای تکراری پیشنهادی، بهطور سیستماتیک این نقاط را در سری شناسایی میکنند.
5.5.3روشهای یادگیری ماشین و دادهکاوی
خوشهبندی و روشهای مبتنی بر چگالی
الگوریتمهایی چون DBSCAN نقاطی را که در نواحی کمچگالی قرار دارند، بهعنوان پرت تشخیص میدهند.
Isolation Forest
با تقسیمبندی تصادفی دادهها، نقاطی را که بهصورت متوسط با عمق کمتر جدا میشوند (یعنی جداسازی آنها آسانتر است) بهعنوان ناهنجاری تشخیص میدهد.
ضریب پرت محلی (Local Outlier Factor – LOF)
چگالی محلی هر نقطه را با چگالی همسایگان نزدیکش مقایسه میکند؛ نقاطی که چگالی بسیار پایینتری دارند، پرت محسوب میشوند.
روشهای مبتنی بر بازسازی (خودرمزگذارها و مشابهها)
یک مدل (مثلاً Autoencoder) روی الگوی «طبیعی» سری آموزش داده میشود؛ نقاطی که خطای بازسازی بالایی دارند، بهعنوان ناهنجاری در نظر گرفته میشوند. این رویکرد برای سریهای زمانی پیچیده و با بعد بالا، بهویژه در ترکیب با LSTM و CNN، بسیار کاربرد دارد.
انتخاب روش مناسب، به ماهیت داده، نوع ناهنجاری مورد انتظار، حجم داده و هدف کاربردی (تشخیص برخط، تحلیل پسینی، توضیحپذیری و…) بستگی دارد.
5.6 راهبردهای مدیریت دادههای پرت در سریهای زمانی
بعد از تشخیص، پرسش اصلی این است که «با این نقاط چه کنیم؟». راهبردهای اصلی عبارتاند از:
حذف (Deletion / Trimming)
- سادهترین کار، حذف مشاهدات پرت است؛ اما در سریهای زمانی، این کار اغلب باعث ایجاد شکاف در توالی و از دست رفتن ساختار زمانی میشود.
- فقط زمانی قابل توصیه است که تقریباً مطمئن باشیم مقدار ثبتشده خطای فاحش است (مثلاً خرابی سنسور) و بتوانیم آن را با درونیابی یا پیشبینی پوشش دهیم.
جایگزینی / انتساب مقدار (Replacement / Imputation)
- روشهای ساده: جایگزینی با میانه یا میانگین نقاط مجاور.
- درونیابی: (Interpolation) درونیابی خطی، اسپلاین یا استفاده از پیشبینی مدل برای نقطهی موردنظر.
- انتساب مبتنی بر مدل: استفاده از مدل سری زمانی برازششده برای پیشبینی مقدار «عادی» در آن زمان و جایگزینی آن با مقدار پرت.
تبدیل داده (Transformation)
- تبدیلهایی مثل لگاریتم، جذر یا Box–Cox میتوانند واریانس را تثبیت و فاصلهی ظاهری پرتها از بقیهی نقاط را کم کنند؛ هرچند خودِ ناهنجاری را حذف نمیکنند.
استفاده از روشهای مقاوم
- بهجای دستکاری داده، از تخمینگرها و مدلهایی استفاده میشود که ذاتاً نسبت به دادههای پرت حساسیت کمتری دارند؛
- مانند M-estimatorها، مدلهای ARIMA مبتنی بر توزیعهای دمسنگین، یا روشهای هموارسازی مقاوم مثل robust .
مدلسازی صریح دادههای پرت
- در تحلیل مداخله، خودِ دادهی پرت و اثر زمانی آن بهعنوان بخشی از مدل در نظر گرفته میشود؛
- این روش، اطلاعات موجود در دادهی پرت را حفظ میکند و معمولاً از نظر آماری دقیقترین رویکرد است، بهویژه زمانی که رویدادهای نادر خود موضوع تحلیل هستند.
انتخاب راهبرد مناسب کاملاً وابسته به زمینه است:
آیا دادهی پرت خطاست یا سیگنال؟ آیا پیشبینی مهمتر است یا توضیح ساختار سری؟ حجم داده چقدر است؟ آیا امکان استفاده از روشهای مقاوم وجود دارد؟
5.7 چالشها و ملاحظات ویژه در سریهای زمانی
تحلیل دادههای پرت در سریهای زمانی با چند چالش کلاسیک مواجه است:
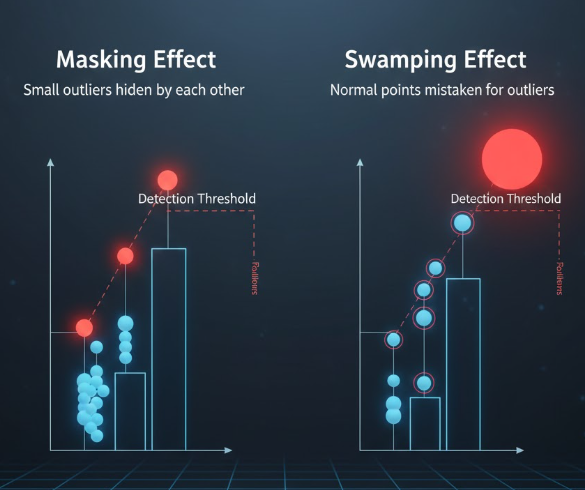
- اثر پوشاندن (Masking)
چند دادهی پرت نزدیک به هم میتوانند یکدیگر را «پنهان» کنند و الگوریتم نتواند آنها را بهعنوان ناهنجاری تشخیص دهد . - اثر غرق کردن (Swamping)
برعکس، وجود یک یا چند نقطهی بسیار دورافتاده میتواند باعث شود نقاط نرمال مجاور، به اشتباه پرت تشخیص داده شوند . - ناایستایی (Non-stationarity)
روندها و فصلیتها میتوانند بهراحتی با دادههای پرت اشتباه گرفته شوند. تمایز میان شکست ساختاری واقعی و یک رویداد موقتی، نیازمند مدلسازی دقیق و اغلب استفاده از دانش دامنه است. - سریهای زمانی چندمتغیره
ممکن است یک نقطه در هیچ بعدی بهتنهایی افراطی نباشد، ولی در فضای چندبعدی یک ناهنجاری حقیقی باشد. این موضوع تشخیص را دشوارتر و نیازمند روشهای چندمتغیره (مثلاً فاصلهی ماهالانوبیس مقاوم) میکند. - انتخاب آستانه
تبدیل امتیاز ناهنجاری به برچسب پرت/نرمال همیشه نیازمند تعیین آستانه است؛ این آستانه، هم به ویژگی داده و هم به هزینهی خطاهای نوع اول و دوم در کاربرد موردنظر وابسته است و نمیتوان آن را کاملاً مکانیکی تعیین کرد.
5.8 روندها و جهتگیریهای آینده در سریهای زمانی
مسئلهی دادههای پرت در سریهای زمانی همچنان یک حوزهی بسیار فعال تحقیقاتی است. برخی جهتگیریهای مهم عبارتاند از:
- بهکارگیری گستردهی یادگیری عمیق (RNN، LSTM، CNN، Transformer، Autoencoderها) برای تشخیص الگوهای پیچیده و ناهنجاری در سریهای زمانی طولانی و با ابعاد بالا؛
- توسعهی الگوریتمهای برخط (Online / Real-time) برای تشخیص ناهنجاری در جریان داده، بهویژه در کاربردهایی مانند نظارت صنعتی، امنیت سایبری و تشخیص تقلب؛
- طراحی روشهای ترکیبی که مزایای رویکردهای آماری، مدلمحور و یادگیری ماشین را با هم تلفیق کنند؛
- و نهایتاً، تمرکز روزافزون بر توضیحپذیری (XAI)، بهگونهای که سیستم نهفقط بگوید «این نقطه پرت است»، بلکه مشخص کند «به چه دلیل» و «کدام ویژگیها» بیشترین نقش را داشتهاند.
نتیجهگیری
دادههای پرت در سریهای زمانی بهدلیل وابستگی مشاهدات به یکدیگر، رفتاری پیچیدهتر از دادههای مقطعی دارند و میتوانند روند، سطح، فصلیت و ساختار سری را بهطور جدی منحرف کنند. انواع مختلف Outlier مانند AO، IO، LS و TC هرکدام اثرات خاصی بر مسیر سری زمانی دارند و تشخیص تفاوت آنها برای جلوگیری از گمراهی مدلها اساسی است.
روشهای تشخیص Outlier در سری زمانی—from تحلیل بصری و شاخصهای آماری تا مدلهای ARIMA و الگوریتمهای یادگیری ماشین—هرکدام تنها بخشی از مسئله را حل میکنند. ترکیب این روشها همراه با تحلیل پسماندها دقیقترین تصویر را ارائه میدهد و کمک میکند مشخص شود یک نقطه واقعاً خطاست یا نشانه رویدادی مهم در فرآیند.
در نهایت، مدیریت Outlier باید بر اساس ماهیت داده و هدف تحلیل انجام شود: گاهی حذف یا اصلاح لازم است، و گاهی مدلسازی صریح آن بهترین راهکار است. آنچه اهمیت دارد این است که Outlierها تنها نویز نیستند؛ آنها پیامهایی درباره رفتار واقعی سیستماند، و تحلیلگر حرفهای کسی است که بتواند این پیامها را درست تفسیر کند.

