مقدمه
شبکههای عصبی بدون توابع فعالسازی، چیزی فراتر از یک مدل خطی ساده نخواهند بود. آنچه به شبکه عصبی توانایی یادگیری الگوهای پیچیده و غیرخطی را میدهد، تابع فعالسازی (Activation Function) است؛ مفهومی کلیدی که نقش تعیینکنندهای در قدرت، سرعت و پایداری یادگیری مدل دارد.
توابع فعالسازی مشخص میکنند که خروجی هر نورون چگونه به لایه بعدی منتقل شود و آیا یک نورون «فعال» شود یا خیر. انتخاب نادرست این توابع میتواند باعث مشکلاتی مانند ناپدید شدن گرادیان، همگرایی ضعیف یا عملکرد نامطلوب مدل شود. در حالی که انتخاب درست آنها میتواند یادگیری شبکه را بهطور چشمگیری بهبود دهد.
در این مقاله، بهصورت جامع با توابع فعالسازی در شبکههای عصبی آشنا میشویم. منطق عملکرد آنها را بررسی میکنیم و پرکاربردترین توابع را با مثالهای واقعی معرفی خواهیم کرد. هدف این است که پس از مطالعه این مطلب، بتوانید با دیدی آگاهانهتر و مسئلهمحور، تابع فعالسازی مناسب را برای هر مدل انتخاب کنید.
تعریف تابع فعالسازی
به زبان ساده، یک تابع فعالسازی تصمیم میگیرد که آیا یک نورون باید فعال شود یا خیر. این یعنی تابع با استفاده از عملیات ریاضی ساده، تشخیص میدهد که آیا ورودیِ یک نورون در فرآیند پیشبینی شبکه اهمیت دارد یا باید نادیده گرفته شود.
نقش اصلی این تابع، استخراج خروجی از مجموعهای از مقادیر ورودی است که به یک گره (Node) یا یک لایه تزریق شدهاند.
گره (Node) چیست؟
برای درک بهتر، بیایید یک لایه به عقب برگردیم. اگر شبکه عصبی را با مغز انسان مقایسه کنیم، هر گره در واقع نسخهای شبیهسازی شده از یک نورون است. این گره، مجموعهای از سیگنالهای ورودی را دریافت میکند که میتوان آنها را معادل محرکهای بیرونی در بدن انسان دانست.
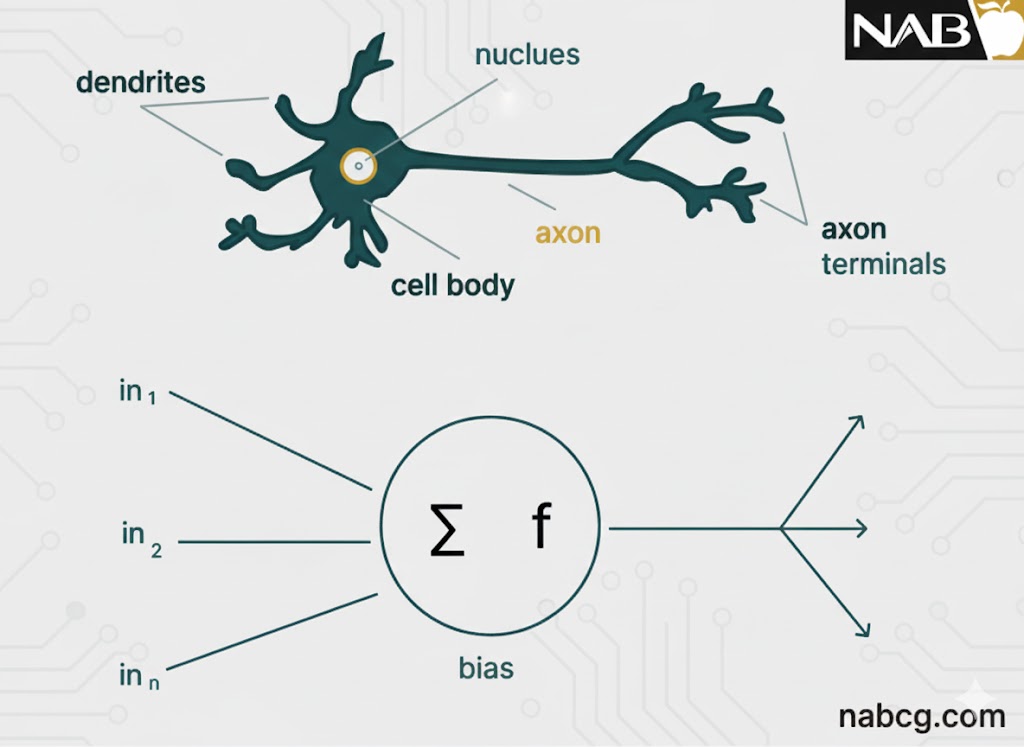
.
بسته به ماهیت و شدت این سیگنالهای ورودی، مغز آنها را پردازش کرده و تصمیم میگیرد که آیا نورون باید فعال (شلیک) شود یا خیر. در دنیای یادگیری عمیق نیز، این دقیقاً وظیفهای است که بر عهده تابع فعالسازی قرار دارد؛ به همین دلیل است که اغلب در شبکههای عصبی مصنوعی از آن به عنوان تابع انتقال (Transfer Function) نیز یاد میشود.
نقش اولیه و حیاتی تابع فعالسازی، تبدیل مجموع وزندار ورودیهای یک گره به یک مقدار خروجی مشخص است تا این مقدار به لایه پنهان بعدی فرستاده شده و یا به عنوان خروجی نهایی سیستم ارائه شود.
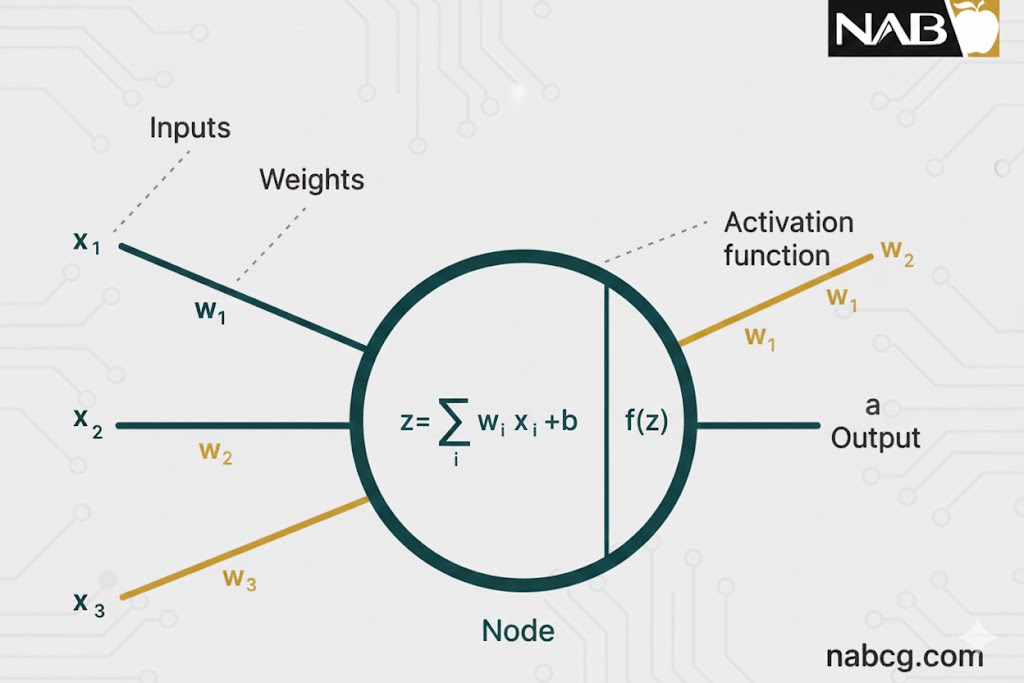
.
ساختار و اجزای اصلی معماری شبکه عصبی
یک شبکه عصبی از نورونهای بههمپیوسته تشکیل شده است که هر کدام با سه مشخصه اصلی شناخته میشوند: وزن (Weight)، بایاس (Bias) و تابع فعالسازی. (Activation Function) این شبکه به طور کلی از سه لایه اصلی تشکیل شده است:
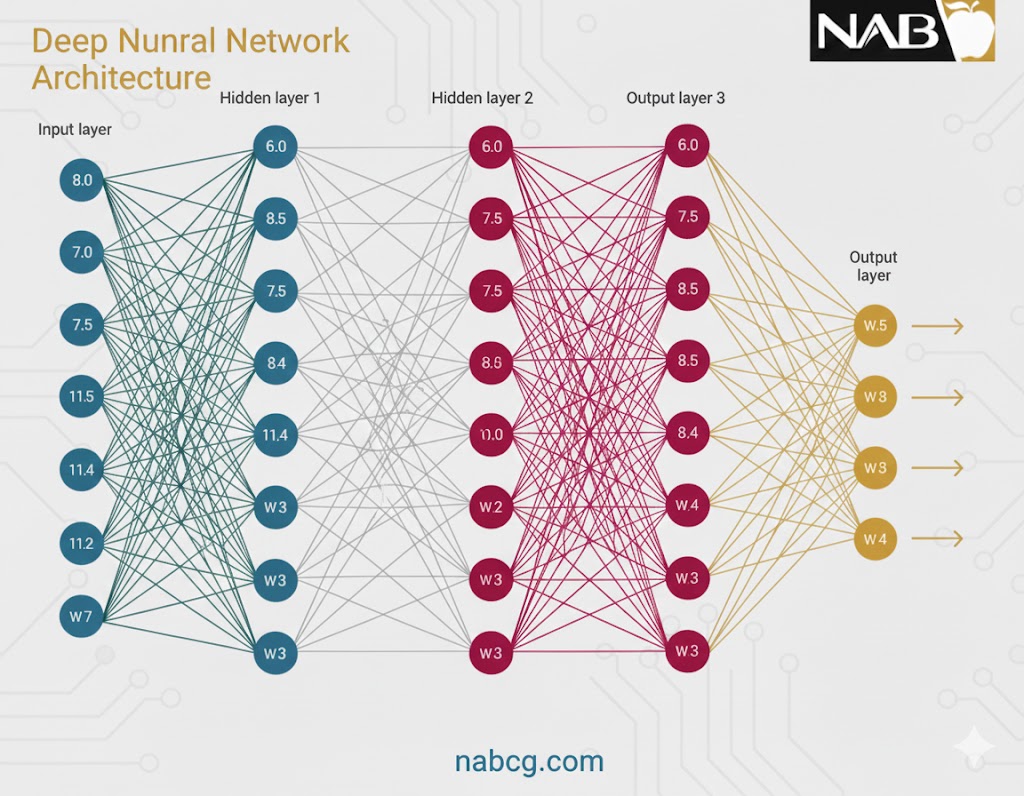
.
۱. لایه ورودی (Input Layer)
این لایه دروازه ورود دادههای خام از دنیای بیرون به داخل سیستم است.
- بدون محاسبات: در این لایه هیچگونه پردازش یا محاسبات ریاضی انجام نمیشود.
- انتقالدهنده: گرههای این لایه صرفاً نقش واسطه را دارند و اطلاعات (ویژگیها یا همان Features) را به لایه پنهان پاس میدهند.
.
۲. لایههای پنهان (Hidden Layers)
همانطور که از نامشان پیداست، گرههای این لایه از دید کاربر پنهان هستند و انتزاع اصلی شبکه را تشکیل میدهند.
- قلب محاسبات: تمامی محاسبات پیچیده ریاضی بر روی ویژگیهای ورودی در این لایه انجام میشود.
- انتقال نتایج: پس از انجام پردازش، لایه پنهان نتایج را برای تصمیمگیری نهایی به لایه خروجی منتقل میکند.
.
۳. لایه خروجی (Output Layer)
این آخرین لایه شبکه است که وظیفه ارائه نتیجه نهایی را بر عهده دارد.
- تبلور یادگیری: این لایه تمامی اطلاعات یاد گرفته شده توسط لایههای پنهان را جمعآوری کرده و مقدار نهایی (پیشبینی) را تحویل میدهد.
وزنها و بایاسها چطور کار میکنند؟
برای اینکه لایهها بتوانند با هم ارتباط برقرار کنند، از دو فاکتور استفاده میکنند:
- وزن(W): نشاندهنده اهمیت یک ویژگی ورودی است. هرچه وزن بیشتر باشد، آن ورودی تاثیر بیشتری بر خروجی دارد.
- بایاس(b): به مدل اجازه میدهد تا انعطافپذیری بیشتری داشته باشد و منحنیهای یادگیری را جابهجا کند تا با دادهها بهتر منطبق شود.
.
انتشار رو به جلو (Feedforward Propagation)
در این مرحله، اطلاعات فقط در یک جهت حرکت میکنند: از لایه ورودی به سمت لایههای پنهان و در نهایت به لایه خروجی.
- نقش تابع فعالسازی: در فرآیند انتشار رو به جلو، تابع فعالسازی مانند یک دروازه ریاضی عمل میکند که بین ورودیِ تغذیهکننده نورون فعلی و خروجیِ ارسالی به لایه بعدی قرار میگیرد.
- تصمیمگیری: این تابع تصمیم میگیرد که آیا اطلاعات دریافتی به قدری مهم هستند که به مرحله بعد منتقل شوند یا خیر.
- خروجی نهایی: نتیجه این مسیر، پیشبینی مدل است (مثلاً تشخیص اینکه عکس متعلق به یک گربه است).
.
انتشار رو به عقب (Backpropagation)
این مرحله جایی است که یادگیری واقعی اتفاق میافتد. پس از اینکه مدل پیشبینی خود را انجام داد، آن را با واقعیت مقایسه میکند.
- محاسبه خطا: تفاوت بین پیشبینی و واقعیت، مقدار خطا را مشخص میکند.
- حرکت معکوس: اطلاعات خطا از لایه خروجی به سمت لایههای عقب حرکت میکنند تا شبکه بفهمد کدام نورونها و وزنها در ایجاد این خطا نقش داشتهاند.
- اصلاح پارامترها: با استفاده از محاسبات مشتق (گرادیان)، وزنها و بایاسها اصلاح میشوند تا در تکرار بعدی، خطا کمتر شود.
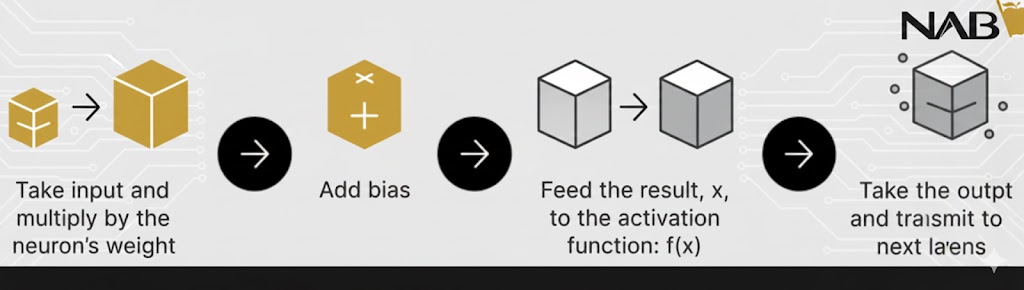
.
آیا میتوانیم بدون تابع فعالسازی کار را انجام دهیم؟
ممکن است این سوال هوشمندانه به ذهن شما هم خطور کرده باشد: استفاده از تابع فعالسازی در هر لایه، یک مرحله اضافی و محاسباتی به فرآیند انتشار رو به جلو (Forward Propagation) اضافه میکند. اگر این کار باعث افزایش پیچیدگی میشود. آیا میتوانیم به سادگی آن را حذف کنیم؟
بیایید با هم سناریویی را تصور کنیم که در آن شبکههای عصبی فاقد هرگونه تابع فعالسازی هستند. در این حالت، هر نورون فقط یک تبدیل خطی (Linear Transformation) روی ورودیها انجام میدهد (یعنی ضرب در وزنها و جمع با بایاس).
اگرچه این کار باعث سادهتر شدن محاسبات ریاضی میشود، اما یک مشکل بزرگ پیش میآید. این شبکه بسیار ضعیف خواهد بود و هرگز توانایی یادگیری الگوهای پیچیده و پنهان در دادهها را نخواهد داشت. در واقع، یک شبکه عصبی بدون تابع فعالسازی، چیزی نیست جز یک مدل رگرسیون خطی ساده.
به همین دلیل است که ما از تبدیلهای غیرخطی استفاده میکنیم؛ این جادوی غیرخطی بودن دقیقاً توسط همین توابع فعالسازی به شبکه تزریق میشود.
چرا وجود توابع فعالسازی غیرخطی حیاتی است؟
برای درک بهتر، بیایید فرآیند یادگیری ماشین را به چند مرحله ساده تقسیم کنیم تا ببینیم چرا غیرخطی بودن ستون فقرات هوش مصنوعی است:
۱. پردازش لایه به لایه دادهها
شبکههای عصبی دادهها را لایه به لایه پردازش میکنند. در هر لایه، یک مجموع وزندار از ورودیها محاسبه شده و با یک عدد بایاس جمع میشود.
۲. بنبستِ محدودیت خطی
اگر تمام لایهها از توابع فعالسازی خطی (y = mx + b) استفاده کنند، هر چقدر هم که لایههای بیشتری روی هم بچینید، خروجی نهایی باز هم یک تابع خطی خواهد بود. مهم نیست شبکه شما چقدر عمیق باشد، خروجی همچنان مثل یک خط صاف عمل میکند و نمیتواند منحنیهای پیچیده را مدلسازی کند.
۳. معرفی دنیای غیرخطی
توابع فعالسازی غیرخطی دقیقاً بعد از مرحله محاسبات خطی در هر لایه وارد عمل میشوند. این توابع، دادههای خطی و خشک را به شکلی انعطافپذیر و منحنی تغییر میدهند (مثلاً تابع سیگموئید خروجی را به شکل یک منحنی S در میآورد).
۴. یادگیری الگوهای فوقپیچیده
به لطف این تبدیلهای غیرخطی، شبکه میتواند الگوهایی را یاد بگیرد که با هیچ خط صافی قابل توصیف نیستند. تصور کنید به جای روی هم چیدن خطکشهای صاف، بخواهید با استفاده از اشکال منحنی و منعطف، یک تصویر پیچیده را خلق کنید.
۵. فراتر از جداسازی ساده
این ویژگی به شبکه اجازه میدهد تا از مرزهای ساده (مثل رگرسیون لجستیک) فراتر برود. حالا سیستم میتواند روابط درهمتنیده و ظریف بین ویژگیهای مختلف داده را کشف کند.
۶. زیربنای ماموریتهای دشوار
در نهایت، همین توابع غیرخطی هستند که به عنوان بلوکهای سازنده عمل میکنند و به شبکههای عصبی قدرت میدهند تا وظایف سنگینی مثل تشخیص چهره، پردازش زبان طبیعی (NLP) و بسیاری از تکنولوژیهای مدرن را به سرانجام برسانند.
بررسی ۳ دسته اصلی توابع فعالسازی در شبکههای عصبی
پس از درک مفاهیم پایه، نوبت به شناخت محبوبترین و پرکاربردترین توابع فعالسازی میرسد که رفتار لایههای شبکه را تعیین میکنند.
۱. تابع پلهای دوگانه (Binary Step Function)
۲. تابع فعالسازی خطی (Linear Activation Function)
۳. توابع فعالسازی غیرخطی (Non-Linear Activation Functions)
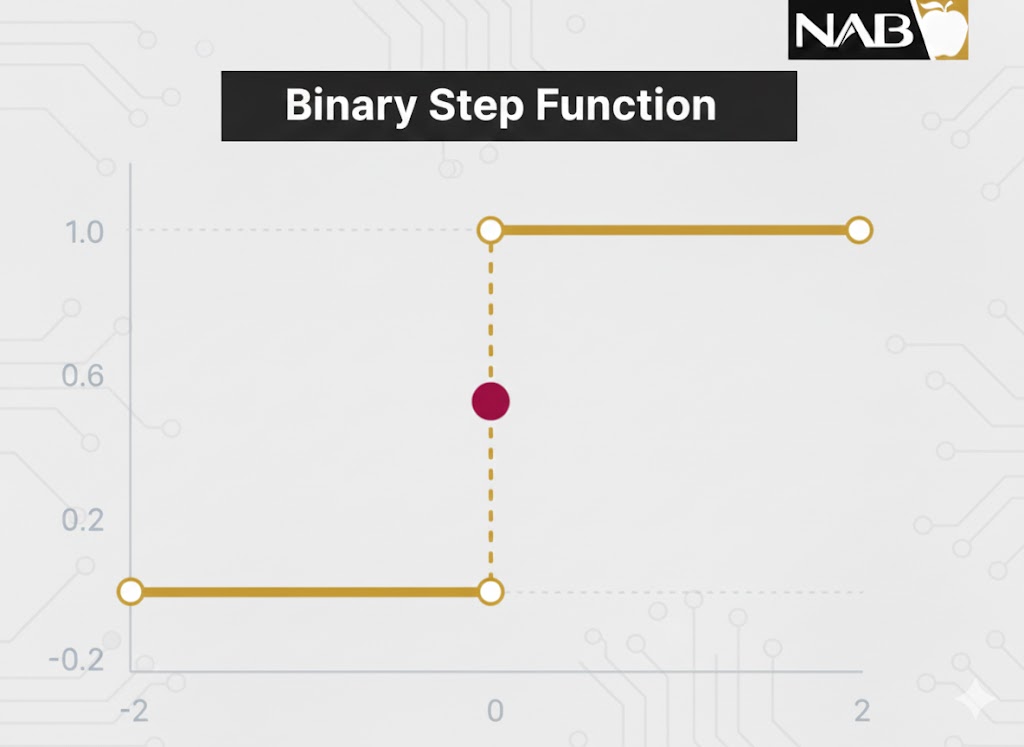
تابع پلهای دوگانه (Binary Step Function)
تعریف و مفهوم
تابع پلهای دوگانه بر اساس یک مقدار آستانه (Threshold) تصمیم میگیرد که آیا یک نورون باید فعال شود یا خیر. ورودی تغذیه شده به تابع با این آستانه مقایسه میشود؛ اگر ورودی بزرگتر از آستانه باشد، نورون فعال شده و در غیر این صورت غیرفعال میماند و سیگنالی به لایه بعدی نمیفرستد.
فرمول ریاضی
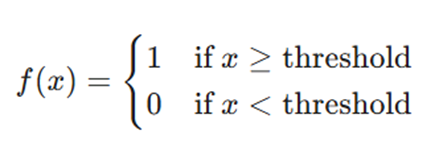
مزایا:
- سادگی بسیار زیاد در پیادهسازی محاسباتی.
- خروجی قطعی (صفر یا یک) که برای تصمیمگیریهای بله/خیر ساده عالی است.
معایب:
- عدم پشتیبانی از خروجیهای چندگانه: برای مسائل طبقهبندی چندکلاسه (Multi-class) قابل استفاده نیست.
- مشکل گرادیان صفر: مشتق این تابع صفر است، که باعث متوقف شدن فرآیند انتشار رو به عقب (Backpropagation) میشود.
کاربرد و مثال
- کاربرد: پرسپترونهای اولیه و مدارهای منطقی ساده.
- مثال: سیستمی که فقط باید تشخیص دهد آیا فشار مخزن از حد مجاز عبور کرده است یا خیر.
.
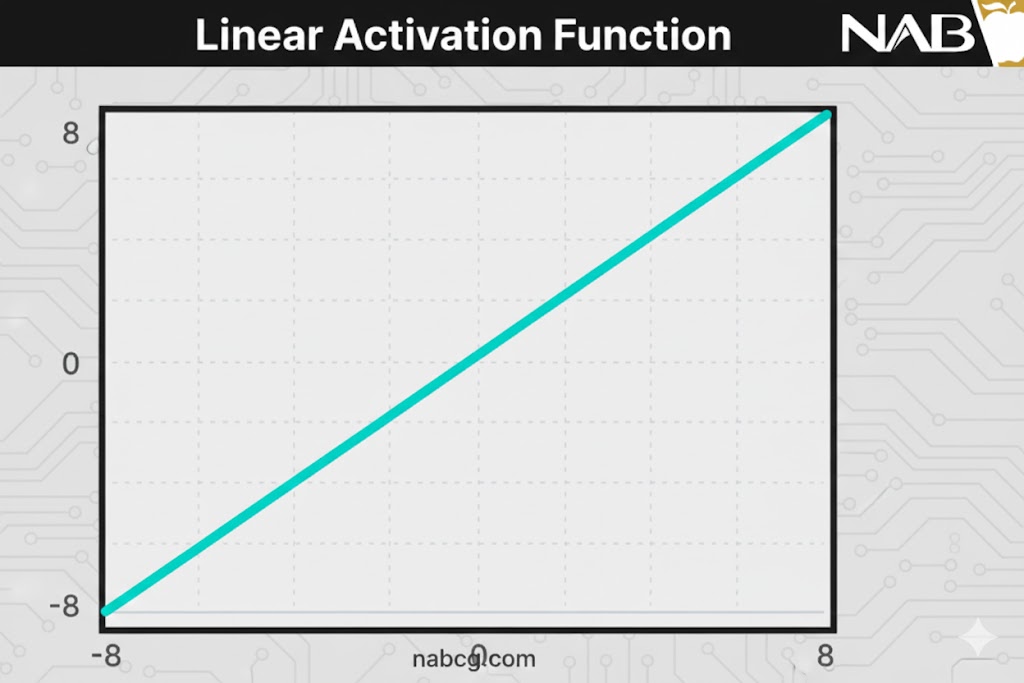
تابع فعالسازی خطی (Linear Activation Function)
تعریف و مفهوم
این تابع که با نامهای “بدون فعالسازی“ یا “تابع همانی” (Identity Function) نیز شناخته میشود، خروجی را دقیقاً متناسب با ورودی تولید میکند. این تابع هیچ تغییری روی مجموع وزندار ورودیها انجام نمیدهد و همان مقداری را که دریافت کرده، بیرون میدهد.
فرمول ریاضی
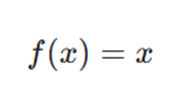
مزایا:
- ایدهآل برای مسائل رگرسیون که خروجی میتواند هر عدد حقیقی باشد.
معایب:
- مشکل در Backpropagation: مشتق این تابع یک عدد ثابت است و هیچ رابطهای با ورودی x ندارد، بنابراین یادگیری پیچیده ممکن نیست.
- فروپاشی لایهها: استفاده از این تابع باعث میشود تمام لایههای شبکه در یک لایه ادغام شوند؛ یعنی خروجی لایه آخر همچنان یک تابع خطی از لایه اول خواهد بود و عمق شبکه بیمعنا میشود.
کاربرد و مثال
- کاربرد: لایه خروجی در مسائل پیشبینی عددی (رگرسیون).
- مثال: پیشبینی قیمت مسکن بر اساس متراژ و ویژگیهای بنا.
.
توابع فعالسازی غیرخطی (Non-Linear Activation Functions)
تعریف و مفهوم
توابع خطی در واقع فقط یک مدل رگرسیون خطی ساده هستند و قدرت ایجاد نگاشتهای پیچیده بین ورودی و خروجی را ندارند. توابع غیرخطی برای حل محدودیتهای مدلهای خطی معرفی شدهاند و به شبکه اجازه میدهند الگوهای درهمتنیده را یاد بگیرد.
چرا توابع غیرخطی ضروری هستند؟
- امکان انتشار رو به عقب: چون مشتق این توابع با ورودی در ارتباط است، میتوان به عقب برگشت و فهمید کدام وزنها نیاز به اصلاح دارند تا پیشبینی بهتری حاصل شود.
- امکان چیدمان لایهها : این توابع اجازه میدهند چندین لایه نورون روی هم قرار گیرند، زیرا خروجی اکنون یک ترکیب غیرخطی از ورودیهایی است که از چندین لایه عبور کردهاند. هر خروجی را میتوان به عنوان یک محاسبه عملکردی در شبکه عصبی نمایش داد.
.
انواع توابع غیرخطی
در ادامه، به بررسی ۱۰ تابع غیرخطی مختلف و ویژگیهای آنها خواهیم پرداخت که شامل مواردی چون Sigmoid، Tanh، ReLU و نسخههای پیشرفتهتر آنها میشود.
۱. تابع فعالسازی سیگموئید یا لجستیک (Sigmoid / Logistic)
۲. تابع تانژانت هیپربولیک (Tanh)
۳. تابع ReLU (واحد اصلاحشده خطی)
۴. تابع Leaky ReLU
۵. تابع (PReLU) Parametric ReLU
۶. تابع واحد خطی نمایی (ELU)
۷. تابع سافتمکس (Softmax)
۸. تابع سویش (Swish)
۹. تابع واحد خطی خطای گاوسی (GELU)
۱۰. تابع واحد خطی نمایی مقیاسشده (SELU)
.
۱. تابع فعالسازی سیگموئید یا لجستیک (Sigmoid / Logistic)
تعریف و مفهوم
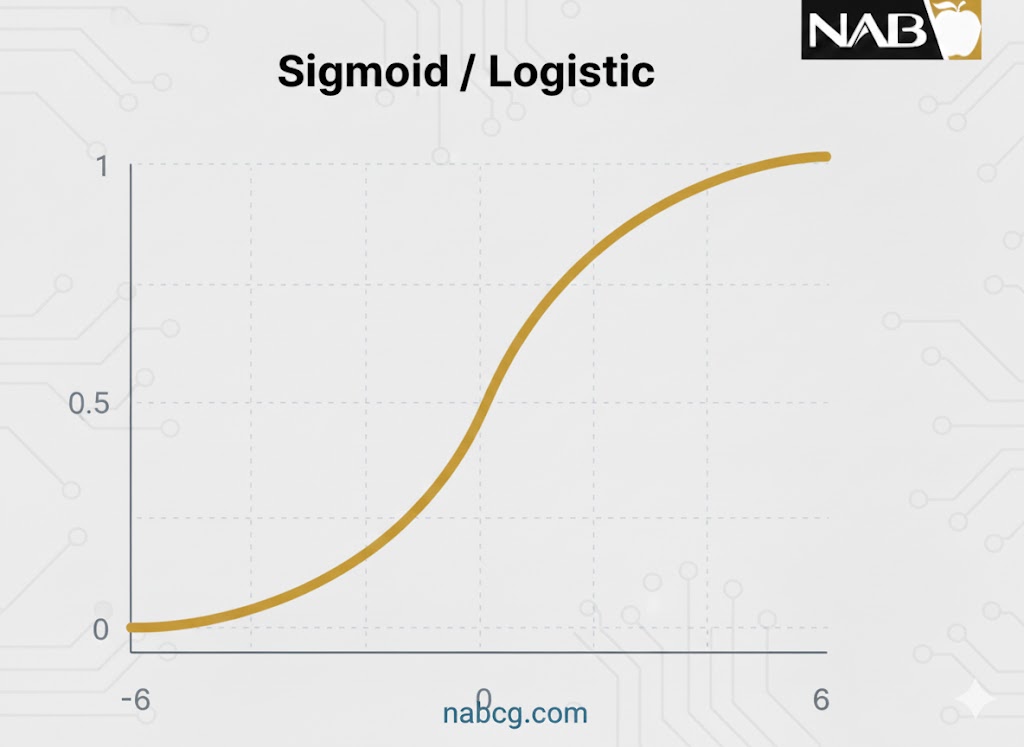
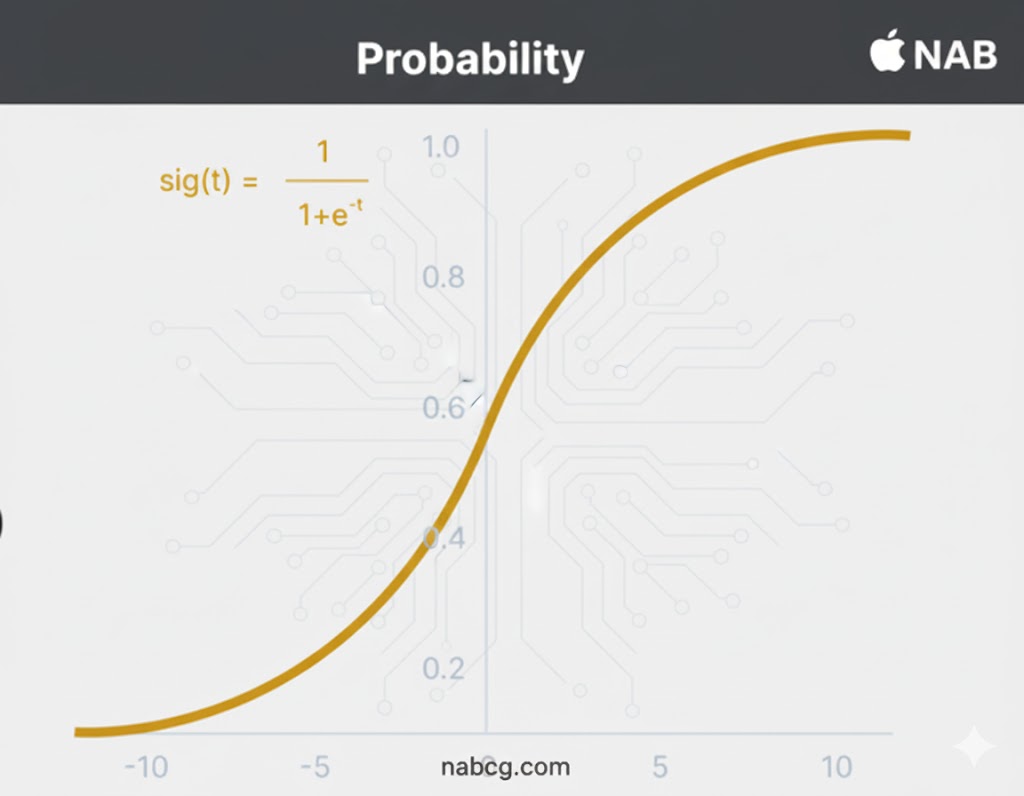
تابع سیگموئید یکی از کلاسیکترین توابع فعالسازی است که هر عدد حقیقی را به عنوان ورودی دریافت کرده و خروجی آن را دقیقا در بازه ۰ تا ۱ قرار میدهد. در این تابع، هرچه ورودی بزرگتر (مثبتتر) باشد، خروجی به ۱.۰ نزدیکتر میشود و هرچه ورودی کوچکتر (منفیتر) باشد، خروجی به ۰.۰ متمایل خواهد بود.
فرمول ریاضی
این تابع با نماد σ (x) نشان داده میشود و فرمول آن به شرح زیر است:
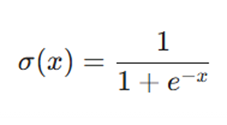
چرا سیگموئید بسیار محبوب است؟
- پیشبینی احتمال: این تابع برای مدلهایی که نیاز به پیشبینی احتمال به عنوان خروجی دارند، بهترین انتخاب است؛ چرا که احتمال همیشه بین ۰ و ۱ تعریف میشود.
- گرادیان نرم(S-Shape): این تابع مشتقپذیر است و یک گرادیان هموار ایجاد میکند که مانع از پرشهای ناگهانی در مقادیر خروجی میشود. این ویژگی در نمودار به صورت یک منحنی S شکل ظاهر میشود.
مزایا:
- درک شهودی بالا برای مسائل طبقهبندی دوگانه. (Binary Classification)
- ایدهآل برای لایههای خروجی که نیاز به خروجی احتمالی دارند.
معایب و محدودیتها:
- مشکل محو شدن گرادیان: مشتق این تابع برابر است با f'(x) = σ (x)(1- σ (x)) . همانطور که در نمودار مشخص است، مقادیر گرادیان فقط در بازه ۳– تا ۳ قابل توجه هستند و در خارج از این بازه، نمودار بسیار تخت میشود. این یعنی برای مقادیر بزرگتر از ۳ یا کوچکتر از ۳-، گرادیان به صفر نزدیک شده، یادگیری شبکه متوقف میشود و شبکه دچار مشکل محو شدن گرادیان میگردد.
- عدم تقارن حول صفر: خروجی این تابع حول صفر متقارن نیست؛ بنابراین خروجی تمام نورونها همواره دارای یک علامت (مثبت) خواهد بود. این موضوع آموزش شبکه عصبی را دشوارتر و ناپایدارتر میکند.
کاربرد و مطالعه موردی
- کاربرد: لایه نهایی در مدلهای تشخیص هرزنامه (Spam Detection) یا تشخیص بیماری (بله/خیر).
- مثال: در یک سیستم تشخیص تقلب بانکی، تابع سیگموئید مشخص میکند که احتمال “تقلب” بودن یک تراکنش چند درصد است (مثلاً ۰.۸۵ یا ۸۵٪).
.
۲. تابع تانژانت هیپربولیک (Tanh)
تعریف و مفهوم
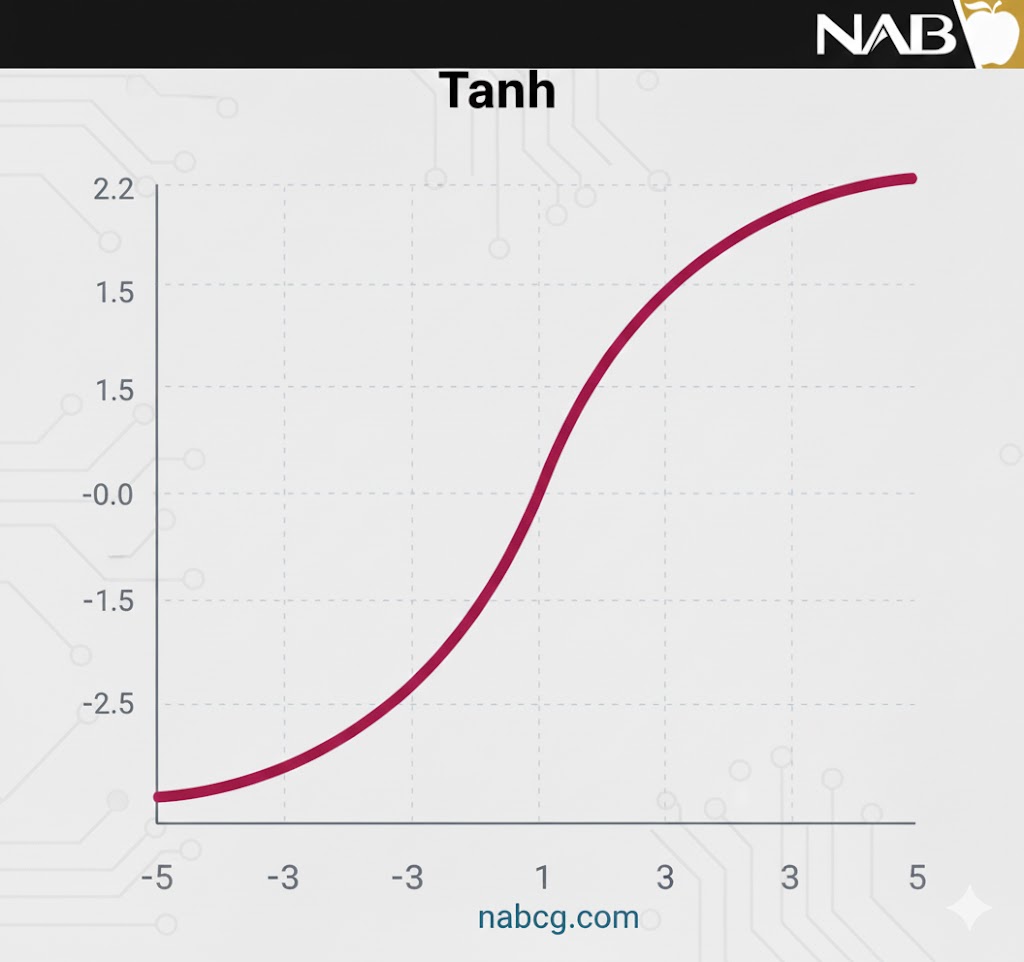
تابع Tanh شباهت بسیار زیادی به تابع سیگموئید دارد و همان منحنی S شکل را نمایش میدهد، با این تفاوت که بازه خروجی آن بین ۱– تا ۱ است. در این تابع، هرچه ورودی بزرگتر (مثبتتر) باشد، خروجی به ۱.۰ نزدیکتر میشود و هرچه ورودی کوچکتر (منفیتر) باشد، خروجی به ۱.۰– متمایل خواهد بود.
فرمول ریاضی
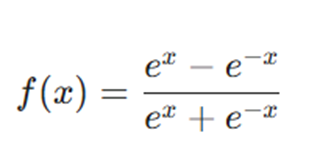
مزایا:
- تمرکز حول صفر: خروجی این تابع حول صفر متمرکز است؛ بنابراین میتوان خروجیها را به راحتی به گروههای به شدت منفی، خنثی و به شدت مثبت نگاشت کرد.
- مناسب برای لایههای پنهان: به دلیل بازه ۱- تا ۱، میانگین خروجی لایههای پنهان به صفر نزدیک میشود که باعث مرکزیت دادهها (Data Centering) و تسهیل یادگیری در لایههای بعدی میگردد.
- برتری بر سیگموئید: اگرچه هر دو با مشکل محو شدن گرادیان روبرو هستند، اما به دلیل مرکزیت حول صفر و عدم محدودیت جهت حرکت گرادیانها، در عمل Tanh همیشه بر سیگموئید ترجیح داده میشود.
معایب:
- محو شدن گرادیان: مشابه سیگموئید، در مقادیر بسیار بزرگ یا بسیار کوچک ورودی، نمودار تخت شده و گرادیان به صفر نزدیک میشود که مانع یادگیری شبکه میگردد.
- شیب تند: گرادیان Tanh نسبت به سیگموئید بسیار تندتر است که میتواند در برخی موارد محاسبات را حساستر کند.
کاربرد و مثال
- کاربرد: لایههای پنهان در شبکههای عصبی کمعمق و مدلهای پردازش زبان طبیعی قدیمی.
- مثال: در تحلیل عواطف (Sentiment Analysis)، Tanh میتواند به خوبی تمایز بین جملات منفی (۱-) و مثبت (۱+) را نشان دهد.
.
۳. تابع ReLU (واحد اصلاحشده خطی)
تعریف و مفهوم
ReLU مخفف Rectified Linear Unit است. با وجود ظاهر خطی، این تابع دارای مشتق بوده و اجازه انتشار رو به عقب را میدهد، در حالی که از نظر محاسباتی بسیار بهینه است. ویژگی کلیدی ReLU این است که همه نورونها را همزمان فعال نمیکند؛ نورونها تنها زمانی فعال میشوند که خروجی بزرگتر از صفر باشد.
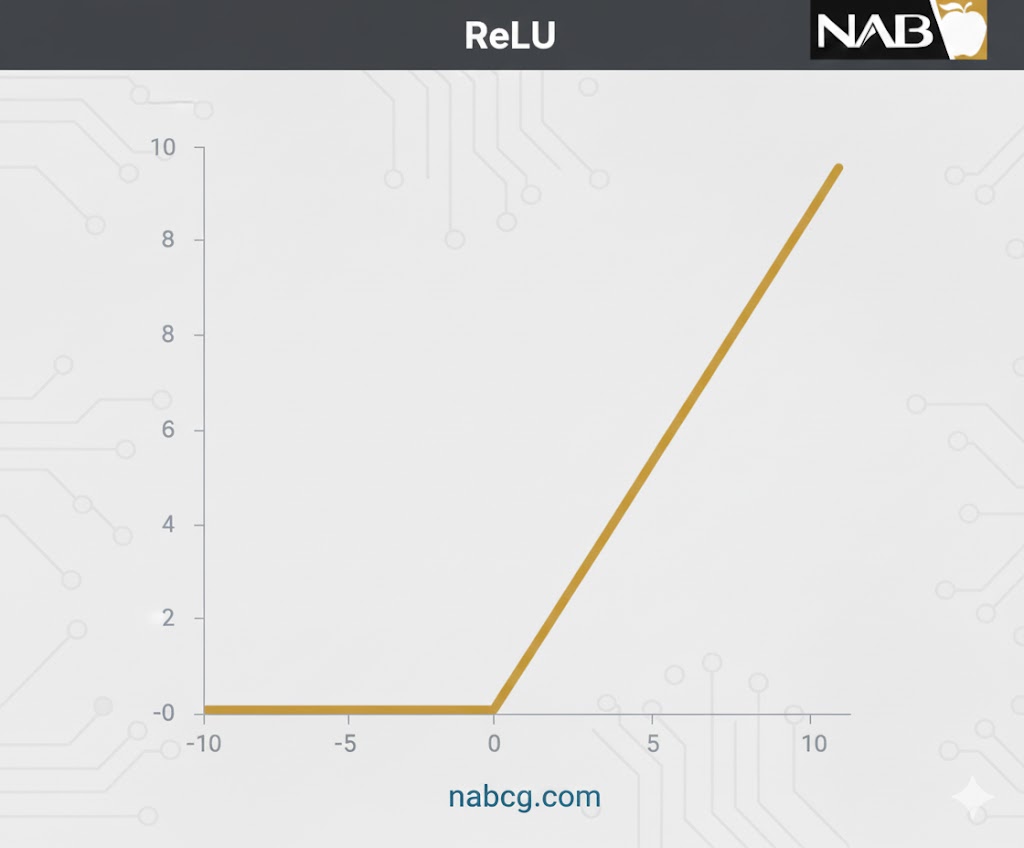
فرمول ریاضی
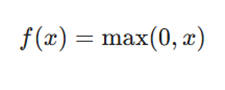
مزایا:
- بهینگی محاسباتی: به دلیل فعالسازی تعداد محدودی از نورونها، این تابع نسبت به Tanh و سیگموئید بسیار سریعتر اجرا میشود.
- همگرایی سریع: به دلیل ماهیت خطی و غیر-اشباع (در ناحیه مثبت)، سرعت رسیدن به کمینه تابع هزینه (Global Minimum) را افزایش میدهد.
معایب:
- مشکل مرگ نورونها: در ناحیه منفی نمودار، مقدار گرادیان صفر میشود. این موضوع باعث میشود در طول Backpropagation، وزنها و بایاسهای برخی نورونها هرگز آپدیت نشوند و نورون عملاً بمیرد.
- کاهش توانایی برازش: تبدیل فوری تمام مقادیر منفی به صفر، توانایی مدل برای یادگیری الگوهای پیچیده از دادههای منفی را کاهش میدهد.
.
۴. تابع Leaky ReLU
تعریف و مفهوم
Leaky ReLU نسخه بهبود یافتهای از ReLU است که برای حل مشکل مرگ نورونها طراحی شده است. این تابع در ناحیه منفی، به جای صفر مطلق، یک شیب مثبت بسیار کوچک دارد.
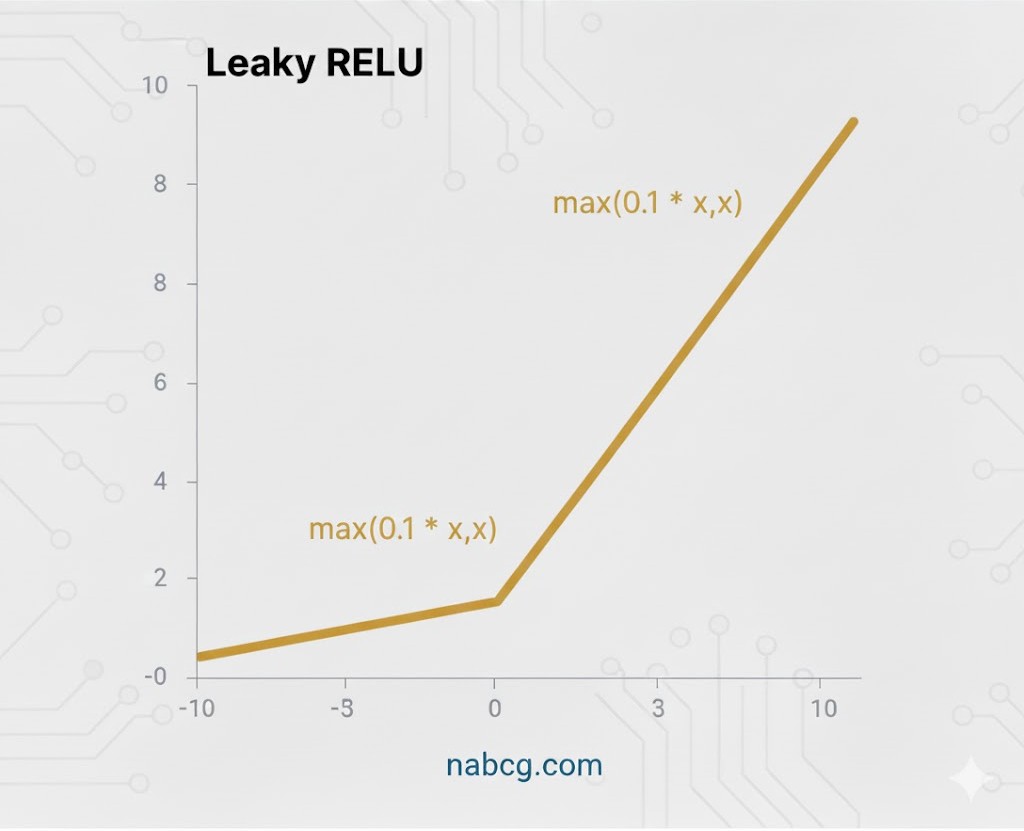
فرمول ریاضی
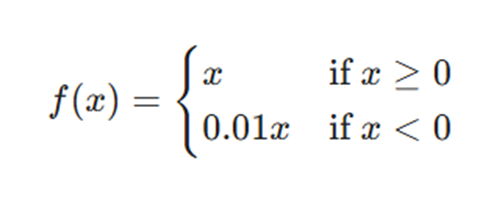
مزایا:
- حل مشکل نورونهای مرده: با ایجاد یک گرادیان غیرصفر در ناحیه منفی، اجازه میدهد وزنها حتی برای ورودیهای منفی نیز بهروزرسانی شوند.
- پشتیبانی از Backpropagation: تمامی مزایای ReLU را دارد و علاوه بر آن فرآیند یادگیری را در ناحیه منفی نیز ممکن میسازد.
معایب:
- عدم ثبات در ناحیه منفی: پیشبینیها برای مقادیر منفی ممکن است همیشه پایدار یا سازگار نباشند.
- یادگیری زمانبر: گرادیان کوچک در ناحیه منفی میتواند فرآیند یادگیری پارامترها را طولانی کند.
.
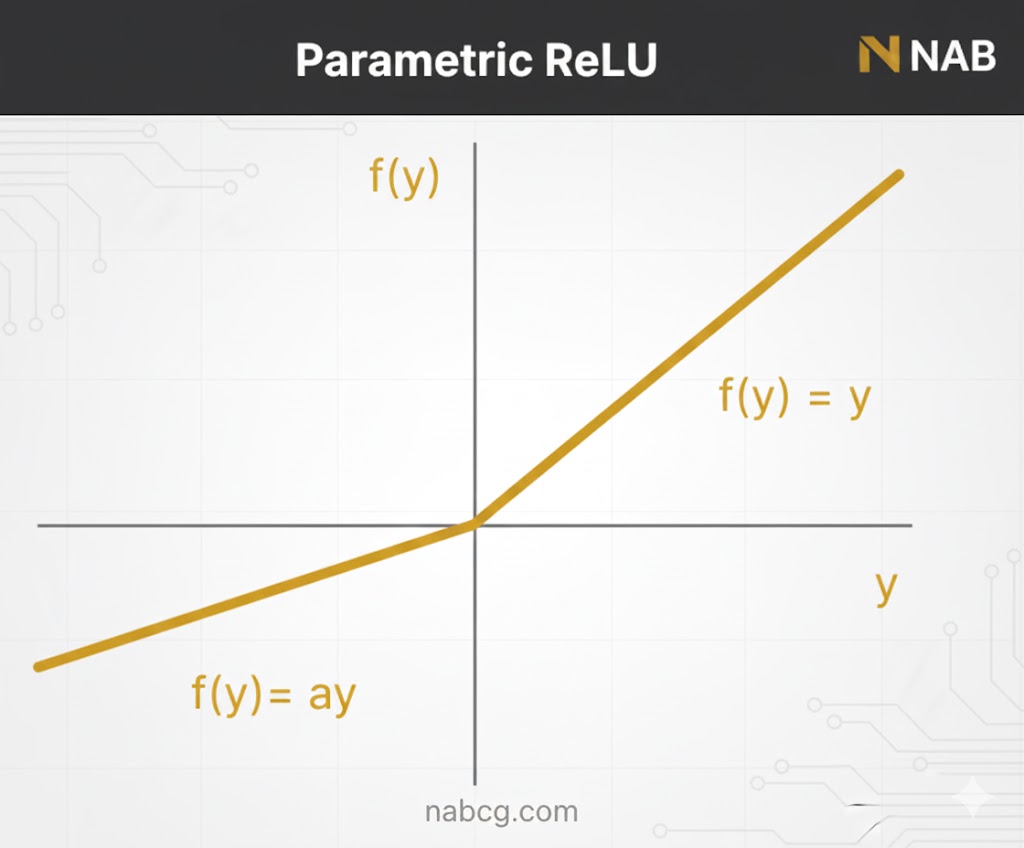
۵. تابع (PReLU) Parametric ReLU
تعریف و مفهوم
Parametric ReLU نوع دیگری از مشتقات ReLU است که هدف آن حل مشکل گرادیان صفر در نیمه منفی محور است. در این تابع، شیب ناحیه منفی یک عدد ثابت نیست، بلکه به عنوان یک پارامتر به نام a در نظر گرفته میشود.
فرمول ریاضی
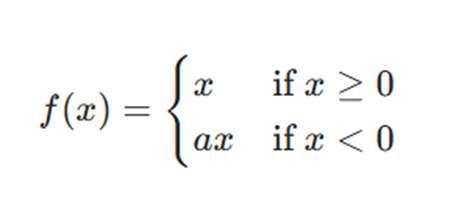
مزایا:
- یادگیری پارامتریک: از طریق Backpropagation، شبکه خودش یاد میگیرد که بهترین مقدار برای شیب ناحیه منفی (a) چقدر باشد.
- جبران شکست Leaky ReLU: زمانی که Leaky ReLU در حل مشکل نورونهای مرده شکست میخورد و اطلاعات به خوبی منتقل نمیشود، PReLU وارد عمل میشود.
معایب:
- عملکرد متغیر: بسته به مقدار یاد گرفته شده برای پارامتر a، ممکن است عملکرد تابع در مسائل مختلف کاملاً متفاوت باشد.
نکته کاربردی: برای ساخت معتبرترین مدلهای یادگیری ماشین، همیشه دادههای خود را به سه دسته آموزش (Train)، اعتبارسنجی (Validation) و تست (Test) تقسیم کنید.
.
۶. تابع واحد خطی نمایی (ELU)
تعریف و مفهوم
ELU یکی از مشتقات قدرتمند ReLU است که بخش منفی تابع را اصلاح میکند. برخلاف Leaky ReLU که از خط صاف در ناحیه منفی استفاده میکند، ELU یک منحنی لگاریتمی را برای تعریف مقادیر منفی به کار میگیرد. فرمول ریاضی
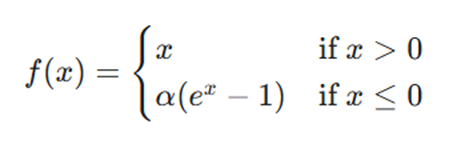
مزایا:
- نرم بودن(Smoothness): برخلاف ReLU که در نقطه صفر تغییر ناگهانی دارد، ELU به آرامی و به شکل نرم به مقدار -α نزدیک میشود.
- حل مشکل مرگ ReLU: با استفاده از منحنی لگاریتمی در ناحیه منفی، از غیرفعال شدن نورونها جلوگیری کرده و به شبکه کمک میکند وزنها را در مسیر درست هدایت کند.
معایب:
- هزینه محاسباتی: به دلیل وجود عملیات نمایی (e^x)، زمان محاسبات نسبت به مدلهای سادهتر افزایش مییابد.
- عدم یادگیری آلفا: مقدار α در این تابع ثابت است و مانند PReLU یاد گرفته نمیشود.
- خطر انفجار گرادیان: در برخی معماریها ممکن است باعث بروز مشکل انفجار گرادیان شود.
.
۷. تابع سافتمکس (Softmax)
تعریف و مفهوم
تابع Softmax را میتوان ترکیبی از چندین تابع سیگموئید دانست که برای محاسبه احتمالات نسبی در مسائل چندکلاسه به کار میرود. در حالی که سیگموئید احتمال یک کلاس را بین ۰ و ۱ میدهد، Softmax احتمال هر کلاس را به گونهای محاسبه میکند که مجموع احتمالات تمام کلاسها برابر با ۱ شود.
فرمول ریاضی
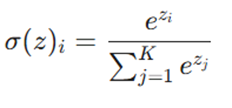
- کاربرد اصلی: لایه آخر شبکههای عصبی برای طبقهبندی چندگانه (Multi-class Classification).
.
۸. تابع سویش (Swish)
تعریف و مفهوم
این تابع یک تابع فعالسازی خود-دروازهبان (Self-gated) است که توسط محققان گوگل توسعه یافته است Swish. در شبکههای عمیق و حوزههای چالشبرانگیزی مثل تشخیص تصویر، عملکردی مشابه یا حتی بهتر از ReLU از خود نشان داده است.
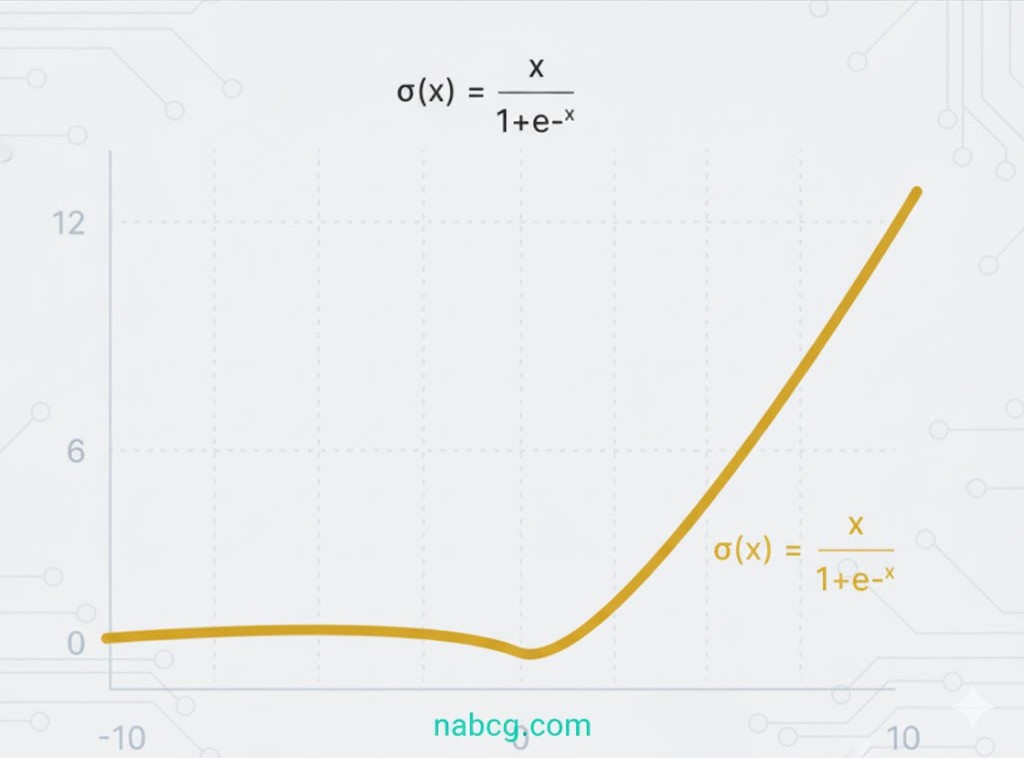
مزایا و ویژگیها
- ساختار ریاضی: از پایین محدود و از بالا نامحدود است؛ یعنی با میل کردن x به سمت منفی بینهایت به یک مقدار ثابت میرسد و با میل کردن به مثبت بینهایت، خروجی نیز بینهایت میشود.
- خمیدگی نرم: برخلاف ReLU که در نقطه صفر تغییر جهت ناگهانی دارد، Swish به آرامی از صفر به سمت مقادیر منفی خم شده و دوباره بالا میآید.
- حفظ الگوهای منفی: مقادیر منفی کوچک که در ReLU حذف میشدند، در Swish حفظ میشوند تا الگوهای پنهان دادهها بهتر استخراج شوند.
.
۹. تابع واحد خطی خطای گاوسی (GELU)
تعریف و مفهوم
تابع GELU با مدلهای تراز اول دنیا مثل BERT، RoBERTa و ALBERT سازگار است. این تابع با ترکیب ویژگیهای Dropout (حذف تصادفی)، Zoneout و ReLU ایجاد شده است.
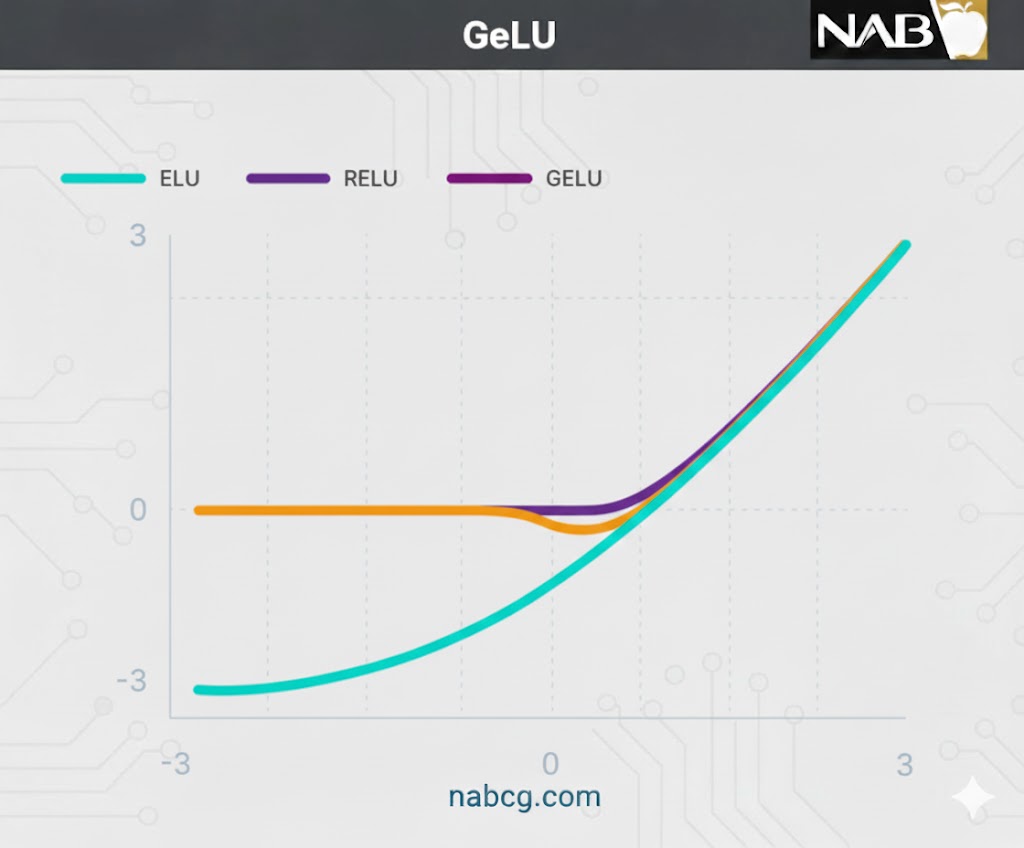
مکانیسم عملکرد
در این تابع، ورودی نورون (x) در مقدار احتمالی توزیع نرمال استاندارد ضرب میشود. از آنجایی که ورودی نورونها (به ویژه با Batch Normalization) معمولاً از توزیع نرمال پیروی میکنند، این انتخاب بسیار هوشمندانه است.
- برتری: عملکرد GELU در حوزههای بینایی ماشین و پردازش زبان طبیعی (NLP) بهتر از ReLU و ELU ارزیابی شده است.
.
۱۰. تابع واحد خطی نمایی مقیاسشده (SELU)
تعریف و مفهوم
SELU در شبکههای خود-نرمالشونده تعریف شده است و وظیفه نرمالسازی داخلی را بر عهده دارد؛ یعنی هر لایه میانگین و واریانس لایه قبلی را حفظ میکند.
مزایا و ویژگیها
- نرمالسازی خودکار: SELU با تنظیم میانگین و واریانس از طریق مقادیر مثبت و منفی، فرآیند نرمالسازی را انجام میدهد که در ReLU به دلیل عدم تولید خروجی منفی غیرممکن بود.
- سرعت همگرایی: نرمالسازی داخلی بسیار سریعتر از نرمالسازی خارجی است و باعث میشود شبکه زودتر به نتیجه برسد.
- نکته: این تابع نسبتاً جدید است و هنوز پتانسیلهای آن در معماریهایی مثل CNN و RNN در حال بررسی بیشتر است.
.
راهنمای گامبهگام انتخاب تابع فعالسازی
به عنوان یک قاعده کلی ، همیشه کار خود را با تابع ReLU شروع کنید. اگر پس از آموزش متوجه شدید که ReLU نتایج بهینهای ارائه نمیدهد، میتوانید به سراغ سایر توابع بروید.
۱. قوانین طلایی برای لایههای پنهان (Hidden Layers)
- قلمرو اختصاصی ReLU: تابع فعالسازی ReLU فقط باید در لایههای پنهان استفاده شود.
- خط قرمز سیگموئید و: Tanh از توابع Sigmoid/Logistic و Tanh در لایههای پنهان استفاده نکنید. این توابع مدل شما را در برابر مشکلاتی مانند محو شدن گرادیان (Vanishing Gradients) در طول آموزش بسیار حساس و آسیبپذیر میکنند.
- شبکههای بسیار عمیق: اگر شبکه عصبی شما دارای عمق بیش از ۴۰ لایه است، تابع Swish انتخاب بهتری خواهد بود.
.
۲. انتخاب بر اساس نوع مسئله (لایه خروجی)
نوع پیشبینی شما تعیین میکند که در لایه آخر از چه تابعی استفاده کنید:
| نوع مسئله پیشبینی | تابع فعالسازی لایه خروجی |
| رگرسیون (تخمین عدد) | خطی (Linear) |
| طبقهبندی دوگانه (بله/خیر) | سیگموئید / لجستیک (Sigmoid) |
| طبقهبندی چندکلاسه (یک از چند) | سافتمکس (Softmax) |
| طبقهبندی چندبرچسبی (چند از چند) | سیگموئید (Sigmoid) |
۳. انتخاب بر اساس معماری شبکه عصبی
معماری انتخابی شما نیز در تعیین تابع لایههای پنهان نقش دارد:
- شبکههای عصبی پیچشی(CNN): برای پردازش تصویر، تابع ReLU انتخاب اول و استاندارد است.
- شبکههای عصبی برگشتی(RNN): برای دادههای سری زمانی و متنی، معمولاً از توابع Tanh و یا Sigmoid استفاده میشود.
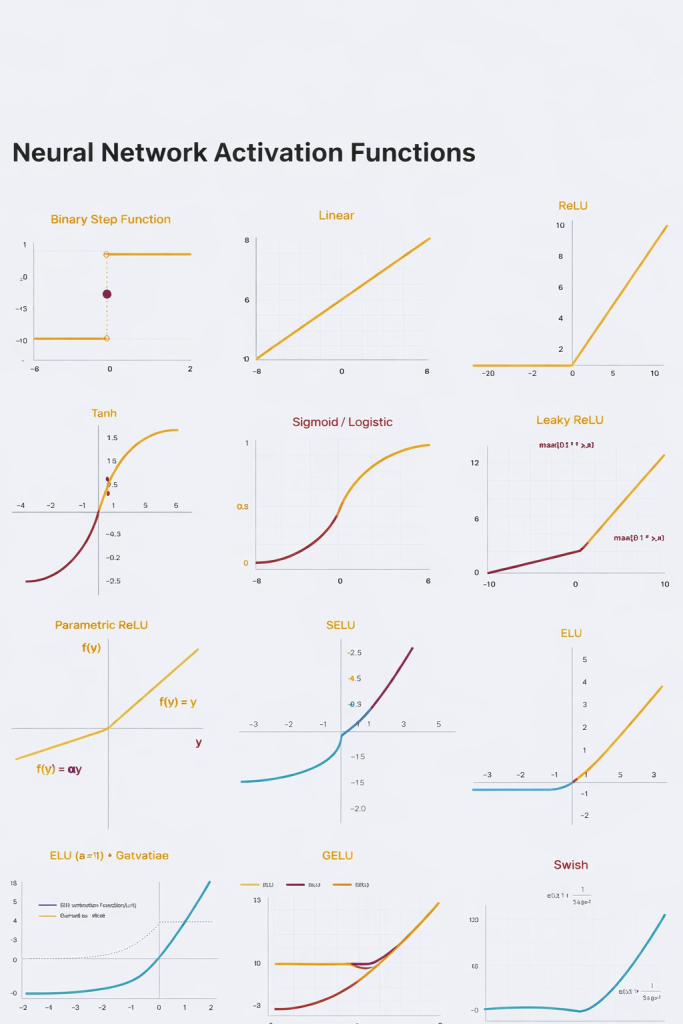
جمع بندی
توابع فعالسازی یکی از اجزای حیاتی شبکههای عصبی هستند که امکان یادگیری روابط غیرخطی را فراهم میکنند و مستقیماً بر کیفیت و پایداری آموزش مدل اثر میگذارند. همانطور که دیدیم، هر تابع فعالسازی رفتار متفاوتی دارد و برای نوع خاصی از مسئله، معماری شبکه یا لایه خروجی مناسبتر است.
در این مقاله بررسی کردیم که چرا توابعی مانند ReLU و خانواده آن در لایههای پنهان محبوباند، چرا Softmax برای مسائل چندکلاسه انتخاب منطقیتری است و چرا توابع قدیمیتری مانند Sigmoid در برخی شرایط با محدودیتهایی مواجه میشوند. این مقایسه نشان داد که هیچ تابع فعالسازی بهطور مطلق بهترین انتخاب نیست و تصمیمگیری باید بر اساس نوع داده و هدف مسئله انجام شود.
در نهایت، شناخت درست توابع فعالسازی به شما کمک میکند شبکههای عصبی را نه بهصورت آزمونوخطا، بلکه با درک عمیق طراحی کنید. این آگاهی، گامی مهم در مسیر حرفهای شدن در یادگیری ماشین و یادگیری عمیق است و پایهای محکم برای درک مباحث پیشرفتهتری مانند گرادیان کاهشی، پسانتشار و بهینهسازی مدلها فراهم میکند.

