مخفف “پارتیشن در اطراف medoids” است. هدف از این الگوریتم یافتن دنباله ای از اشیاء به نام medoids است که در مرکز در خوشه ها قرار دارند. اشیاء
که به طور آزمایشی به عنوان medoid تعریف می شوند، در مجموعه S از اشیاء انتخاب شده قرار می گیرند.
اگر O مجموعه ای از اشیاء باشد که مجموعه U = O – S مجموعه ای از اشیاء انتخاب نشده است.
هدف این الگوریتم به حداقل رساندن میانگین عدم تشابه اشیا است
به نزدیکترین شی انتخاب شده خود. به طور معادل، می توانیم مجموع مقدار را به حداقل برسانیم
تفاوت بین شی و نزدیکترین شی انتخاب شده آنها.
هدف این الگوریتم یافتن دنباله ای از اشیا بنام Mediods است که در مرکز خوشه قرار میگیرند
هدف این الگوریتم به حداقل رساندن میانگین عدم تشابه اشیا به نزدیک ترین شئی انتخاب شده آنهاست
این الگوریتم دو فاز دارد :
- BUILD
در فاز اول، BUILD، مجموعهای از k شیء برای یک اولیه انتخاب میشوند
مجموعه S.
- SWAP
در فاز دوم، SWAP، یکی سعی می کند کیفیت خوشه بندی را با مبادله اشیاء انتخاب شده با اشیای انتخاب نشده بهبود بخشد.
هدف این الگوریتم به حداقل رساندن میانگین عدم تشابه اشیا است
ه نزدیکترین شی انتخاب شده خود. به طور معادل، می توانیم مجموع مقدار را به حداقل برسانیم
تفاوت بین شی و نزدیکترین شی انتخاب شده آنها.
برای هر شی p دو عدد را حفظ می کنیم:
Dp، عدم تشابه بین p و نزدیکترین شی در S،
Ep، عدم تشابه بین p و دومین شی نزدیک در S.
📌 مرحله BUILD شامل مراحل زیر است:
- S را با اضافه کردن یک شی که مجموع فواصل تمام اشیاء دیگر حداقل است، مقداردهی کنید.
- یک شی i ∈ U را به عنوان یک کاندید برای گنجاندن در مجموعه اشیاء انتخاب شده در نظر بگیرید.
- برای یک شی j ∈ U − {i} Dj را محاسبه کنید، عدم تشابه بین j و نزدیکترین شی در S.
- اگر Dj > d(i, j) شیء j در تصمیم گیری برای انتخاب شیء i نقش دارد (زیرا کیفیت خوشه بندی ممکن است سودمند باشد)؛ اجازه دهید Cji = max{Dj −
d(j، i)، 0}.
- سود کل بدست آمده را با افزودن i به S به صورت gi =P محاسبه کنید
آن شی i را انتخاب کنید که gi را به حداکثر می رساند اجازه دهیدS := S ∪ {i} و U = U − {i}.
این مراحل تا زمانی انجام می شوند که k شیء انتخاب شوند. تصمیمات اتخاذ شده در ارزیابی شی i در شکل 1 نشان داده شده است. فاز دوم، SWAP، تلاش می کند مجموعه اشیاء انتخاب شده را بهبود بخشد

Example
مجموعه نقاط ما :

طرح پراکنده:
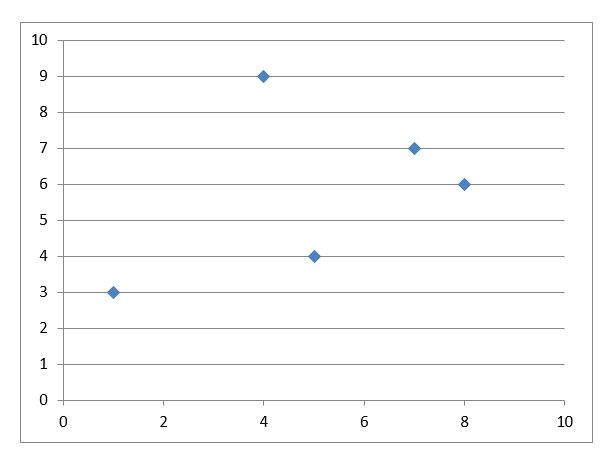
اگر k به عنوان 2 داده شود، باید نقاط داده را به 2 خوشه تقسیم کنیم.
- Mediods اولیه: M1 (1، 3) و M2 (4، 9)
- محاسبه فاصله ها > فاصله منهتن: |x1 – x2| + |y1 – y2|
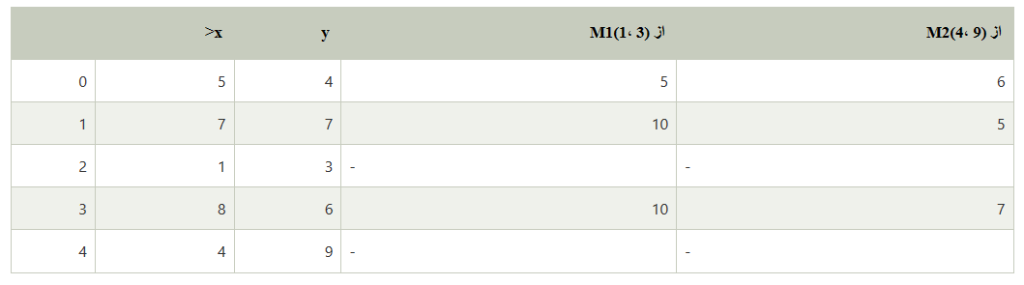
خوشه 1: 0
خوشه 2: 1، 3
محاسبه کل هزینه:
(5) + (5 + 7) = 17
mediods تصادفی: (5، 4)
M1 (5، 4) و M2 (4، 9):

خوشه 1: 2، 3
خوشه 2: 1
محاسبه کل هزینه:
(5 + 5) + 5 = 15
کمتر از هزینه
قبلی medoid جدید: (5، 4).
M1 (5، 4) و M2 (7، 7)

خوشه 1: 2
خوشه 2: 3، 4
محاسبه کل هزینه:
(5) + (2 + 5) = 12
کمتر از هزینه
قبلی medoid جدید: (7، 7).
M1 (7، 7) و M2 (8، 6)

خوشه 1: 4
خوشه 2: 0، 2
محاسبه کل هزینه:
(5) + (5 + 10) = 20
بیشتر از هزینه
قبلی UNDO
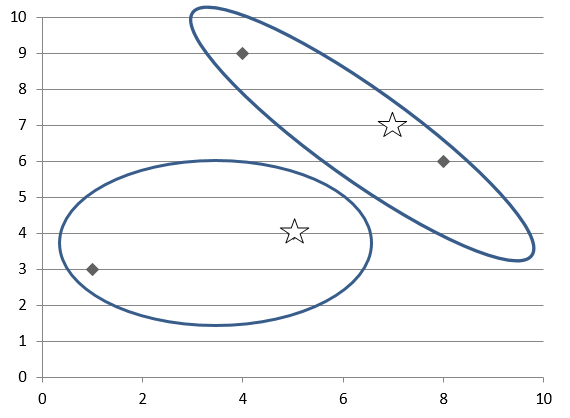
از این رو، medoids نهایی: M1 (5، 4) و M2 (7، 7)
خوشه 1: 2
خوشه 2: 3، 4
هزینه کل: 12
خوشه:
محدودیت PAM:
پیچیدگی زمانی: O(k * (n – k)2)
ترکیبات ممکن برای هر گره: k* (n – k)
هزینه برای هر محاسبه: (n – k)
هزینه کل: k * (n – k) 2
از این رو، PAM مناسب است و توصیه می شود برای مجموعه داده های کوچک استفاده شود.




